Opérations sur les dérivées

- Les résultats de cette section sont à connaître par c
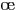 ur : ils vous permettent de calculer les dérivées de toutes les fonctions que vous rencontrerez, à partir d'un petit nombre de dérivées usuelles.
ur : ils vous permettent de calculer les dérivées de toutes les fonctions que vous rencontrerez, à partir d'un petit nombre de dérivées usuelles.
- Théorème 1 Soient
 et
et  deux fonctions définies sur un intervalle
deux fonctions définies sur un intervalle  contenant
contenant  . On suppose que
. On suppose que  et
et  sont dérivables en
sont dérivables en  . Alors :
. Alors :
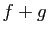 est dérivable en
est dérivable en  , de dérivée
, de dérivée 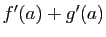
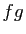 est dérivable en
est dérivable en  , de dérivée
, de dérivée 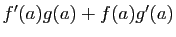 .
.
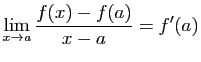 et
et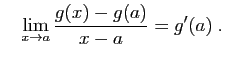
- Écrivons le taux d'accroissement de la somme.
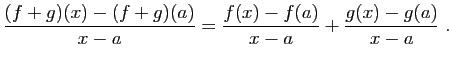 Comme la limite de la somme est la somme des limites, le résultat s'ensuit.
Comme la limite de la somme est la somme des limites, le résultat s'ensuit. - Écrivons le taux d'accroissement du produit.
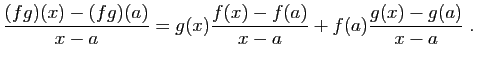 Comme
Comme est dérivable, elle est continue en
est dérivable, elle est continue en  , donc
, donc 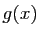 tend vers
tend vers 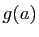 quand
quand  tend vers
tend vers  . La limite d'un produit est le produit des limites, idem pour la somme. D'où le résultat.
. La limite d'un produit est le produit des limites, idem pour la somme. D'où le résultat.
Le théorème 1, combiné avec la proposition 3, entraîne en particulier que toute fonction polynôme est dérivable sur  .
.
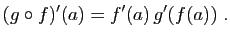
- Théorème 2 Soit
 une fonction définie sur un intervalle ouvert
une fonction définie sur un intervalle ouvert  de
de  , dérivable en
, dérivable en  . Soit
. Soit  une fonction définie sur un intervalle ouvert contenant
une fonction définie sur un intervalle ouvert contenant 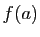 , dérivable en
, dérivable en 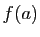 . Alors la composée
. Alors la composée 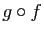 est dérivable en
est dérivable en  , de dérivée :
, de dérivée :
- Démonstration : Par hypothèse, les taux d'accroissement de
 en
en  et de
et de  en
en 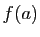 convergent :
convergent :
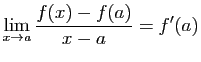 et
et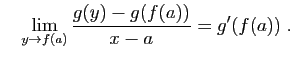
- C1 :
 est continue en
est continue en  ,
,- C2 :
- si
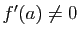 alors
alors 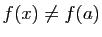 au voisinage de
au voisinage de  ,
, - C3 :
- le taux d'accroissement de
 est borné au voisinage de
est borné au voisinage de 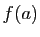 .
.
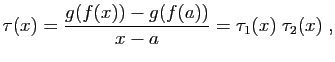
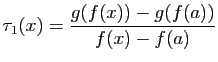 et
et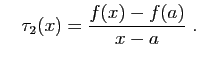
Considérons d'abord le cas où 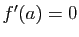 . Dans ce cas,
. Dans ce cas, 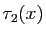 tend vers 0, et comme conséquence de C1 et C3, il existe un intervalle
tend vers 0, et comme conséquence de C1 et C3, il existe un intervalle 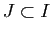 et une constante
et une constante  telle que :
telle que :
Considérons maintenant le cas où 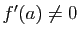 . Comme conséquence de C2,
. Comme conséquence de C2, 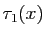 est bien défini au voisinage de
est bien défini au voisinage de
- Dérivées successives
Etant donné un intervalle ouvert 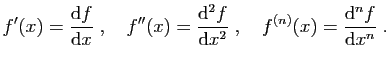
- Définition 5 Soit
 une fonction définie sur un intervalle
une fonction définie sur un intervalle  de
de  . On dit que
. On dit que  est de classe
est de classe 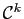 sur
sur  , ou encore
, ou encore  est
est 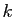 fois continûment dérivable, si elle admet une dérivée
fois continûment dérivable, si elle admet une dérivée 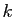 -ième continue sur
-ième continue sur  .
.
toutes les fonctions usuelles sont de classe 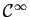
sur les intervalles ouverts où elles sont définies.
La formule de Leibniz, très proche de la formule du binôme de Newton, exprime la dérivée  -ième d'un produit à d'aide des dérivées successives des composantes.
-ième d'un produit à d'aide des dérivées successives des composantes.
- Proposition 5 Si
 et
et  sont deux fonctions de
sont deux fonctions de  dans
dans  ,
,  fois dérivables sur un intervalle
fois dérivables sur un intervalle  , alors le produit
, alors le produit 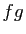 est
est  fois dérivable sur
fois dérivable sur  et :
et :
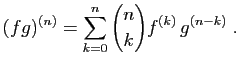 | (1) |
- Démonstration : par récurrence sur
 . Puisque par définition
. Puisque par définition 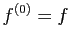 , la formule est vraie pour
, la formule est vraie pour 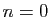 . Supposons qu'elle est vraie pour
. Supposons qu'elle est vraie pour  . Si
. Si  et
et  sont dérivables
sont dérivables 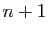 fois sur
fois sur  , alors pour tout
, alors pour tout 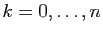 , le produit
, le produit 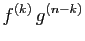 est dérivable et sa dérivée est :
est dérivable et sa dérivée est :
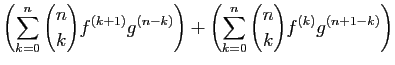 | |||
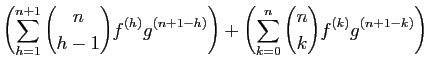 | |||
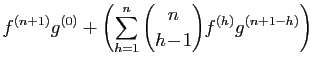 | |||
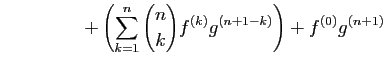 | |||
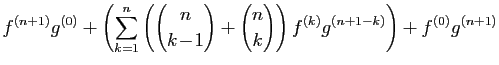 | |||
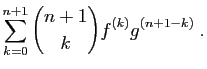 |
Pour la dernière égalité, nous avons appliqué la formule du triangle de Pascal. La formule est vraie pour
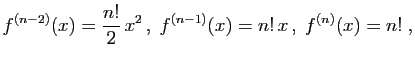
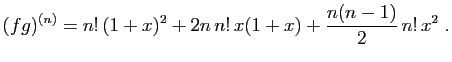
- Le produit de deux fonctions d'une variable réelle
 et
et  définies et dérivables jusqu'à l'ordre
définies et dérivables jusqu'à l'ordre  sur un intervalle
sur un intervalle  est dérivable jusqu'à l'ordre
est dérivable jusqu'à l'ordre  . La formule de Leibniz fournit sa dérivée d'ordre
. La formule de Leibniz fournit sa dérivée d'ordre  donnée par :
donnée par :
 et
et  définies et dérivables jusqu'à l'ordre
définies et dérivables jusqu'à l'ordre  sur un intervalle
sur un intervalle  est dérivable jusqu'à l'ordre
est dérivable jusqu'à l'ordre  . La formule de Leibniz fournit sa dérivée d'ordre
. La formule de Leibniz fournit sa dérivée d'ordre  donnée par :
donnée par :
où les nombres entiers 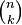 sont les coefficients binomiaux, et où l'on convient que la « dérivée zéro-ième » de f, notée
sont les coefficients binomiaux, et où l'on convient que la « dérivée zéro-ième » de f, notée 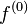 , est la fonction f elle-même.
, est la fonction f elle-même.
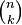 sont les coefficients binomiaux, et où l'on convient que la « dérivée zéro-ième » de f, notée
sont les coefficients binomiaux, et où l'on convient que la « dérivée zéro-ième » de f, notée 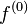 , est la fonction f elle-même.
, est la fonction f elle-même.
- Théorème des accroissements finis
En un point où la dérivée d'une fonction s'annule, les accroissements de la fonction sont négligeables devant les accroissements de la variable. Souvent, c'est un point où les variations de la fonction changent de sens, donc un maximum ou un minimum.
Définition 6 Soit  une fonction de
une fonction de  dans
dans  , définie sur un intervalle ouvert
, définie sur un intervalle ouvert  . Soit
. Soit  un point de
un point de  . On dit que
. On dit que  est un
est un
- maximum local de
 si
si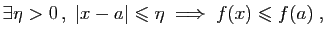
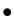
- minimum local de
 si
si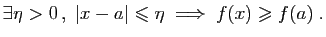
Insistons sur l'adjectif local. Il suffit que la valeur de  en
en  soit la plus grande des valeurs prises par
soit la plus grande des valeurs prises par  sur un petit intervalle autour de
sur un petit intervalle autour de  pour que
pour que  soit un maximum local. Cette valeur n'est pas nécessairement la plus grande prise par
soit un maximum local. Cette valeur n'est pas nécessairement la plus grande prise par  sur tout son domaine de définition (voir le graphe de la figure 3).
sur tout son domaine de définition (voir le graphe de la figure 3).
Théorème 4 Soit  une fonction de
une fonction de  dans
dans  , définie sur un intervalle ouvert
, définie sur un intervalle ouvert  . Si
. Si  présente un extremum (maximum ou minimum) local en un point
présente un extremum (maximum ou minimum) local en un point  de
de  , et si
, et si  est dérivable en
est dérivable en  , alors
, alors 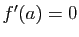 .
.
Démonstration : Si  est un minimum local de
est un minimum local de  , alors c'est un maximum local de
, alors c'est un maximum local de 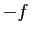 : quitte à remplacer
: quitte à remplacer  par
par 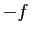 , nous pouvons supposer que
, nous pouvons supposer que  est un maximum local.
est un maximum local.
Donc pour tout  dans l'intervalle
dans l'intervalle 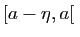 ,
,
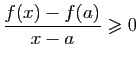 donc
donc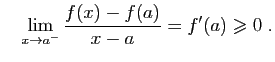
Pour tout  dans l'intervalle
dans l'intervalle ![$ ]a,a+\eta[ $](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img180.gif) ,
,
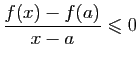 donc
donc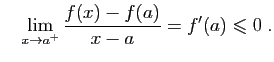
D'où le résultat. Reprenons l'exemple de la figure 2 :
Reprenons l'exemple de la figure 2 : 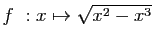 . La dérivée est :
. La dérivée est :
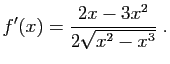
Elle s'annule en 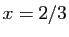 , et
, et  admet effectivement un maximum en ce point. Mais savoir que
admet effectivement un maximum en ce point. Mais savoir que 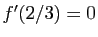 permet seulement d'affirmer que la tangente en ce point est horizontale. Il se pourrait que la dérivée en un point soit nulle sans que la fonction admette un extremum en ce point : par exemple la fonction
permet seulement d'affirmer que la tangente en ce point est horizontale. Il se pourrait que la dérivée en un point soit nulle sans que la fonction admette un extremum en ce point : par exemple la fonction 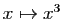 en 0. D'autre part, une fonction peut présenter un extremum en
en 0. D'autre part, une fonction peut présenter un extremum en  , sans être dérivable en ce point (par exemple la fonction
, sans être dérivable en ce point (par exemple la fonction 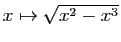 en 0).
en 0).
Voici un autre exemple (figure 3). Soit  la fonction définie par :
la fonction définie par :
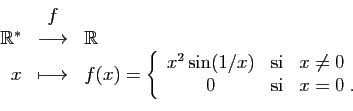
![\includegraphics[width=8cm]{x2sin1}](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img189.gif) |
Le taux d'accroissement de  en 0 est
en 0 est 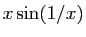 , qui tend vers 0. La dérivée de
, qui tend vers 0. La dérivée de  en 0 est donc nulle. Pourtant, tout intervalle contenant 0, contient aussi des valeurs positives, et des valeurs négatives (et aussi une infinité d'extrema locaux). Nous allons appliquer le théorème 4, pour démontrer le théorème de Rolle.
en 0 est donc nulle. Pourtant, tout intervalle contenant 0, contient aussi des valeurs positives, et des valeurs négatives (et aussi une infinité d'extrema locaux). Nous allons appliquer le théorème 4, pour démontrer le théorème de Rolle.
Théorème 5 Soient  et
et 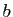 deux réels tels que
deux réels tels que 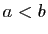 . Soit
. Soit  une fonction de
une fonction de ![$ [a,b]$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img193.gif) dans
dans  , continue sur
, continue sur ![$ [a,b]$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img193.gif) , dérivable sur
, dérivable sur ![$ ]a,b[ $](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img194.gif) . Si
. Si 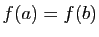 , alors la dérivée de
, alors la dérivée de  s'annule sur
s'annule sur ![$ ]a,b[ $](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img194.gif) .
.
Démonstration : Une application continue sur intervalle fermé borné, atteint sa borne inférieure 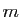 et sa borne supérieure
et sa borne supérieure 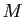 : il existe
: il existe ![$ c_1,
c_2\in[a,b]$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img198.gif) tels que pour tout
tels que pour tout![$ x\in [a,b]$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img199.gif) ,
,
Si 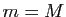 , l'application
, l'application  est constante sur
est constante sur ![$ [a,b]$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img193.gif) , et sa dérivée est identiquement nulle. Si
, et sa dérivée est identiquement nulle. Si 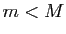 , alors l'une au moins de ces deux valeurs est différente de
, alors l'une au moins de ces deux valeurs est différente de 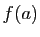 (et donc de
(et donc de 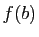 ). Si
). Si 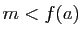 , alors
, alors ![$ c_1\in ]a,b[$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img205.gif) est un minimum pour
est un minimum pour  , et donc
, et donc 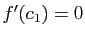 , d'après le théorème précédent. Si
, d'après le théorème précédent. Si 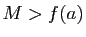 , alors
, alors 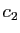 est un maximum pour
est un maximum pour  , et donc
, et donc 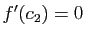 .
.
![\includegraphics[width=8cm]{rolle}](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img210.gif) |
![\includegraphics[width=8cm]{accfini}](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img211.gif) |
On en déduit le résultat le plus important de cette section, le théorème des accroissements finis.
Théorème 6 Soient  et
et 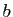 deux réels tels que
deux réels tels que 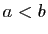 . Soit
. Soit  une fonction de
une fonction de ![$ [a,b]$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img193.gif) dans
dans  , continue sur
, continue sur ![$ [a,b]$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img193.gif) , dérivable sur
, dérivable sur ![$ ]a,b[ $](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img194.gif) .
.
![$\displaystyle \exists c\in ]a,b[\;,\quad \frac{f(b)-f(a)}{b-a}=f'(c)\;.
$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img212.gif)
Démonstration : Considérons la fonction  , qui à
, qui à ![$ x\in [a,b]$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img199.gif) associe
associe
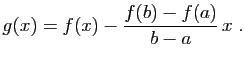
La fonction  est continue sur
est continue sur ![$ [a,b]$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img193.gif) , dérivable sur
, dérivable sur ![$ ]a,b[ $](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img194.gif) . De plus, elle prend la même valeur en
. De plus, elle prend la même valeur en  et
et 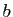 :
:
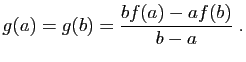
D'après le théorème de Rolle, la dérivée de  s'annule en un point
s'annule en un point 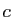 de
de ![$ ]a,b[ $](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img194.gif) .
.
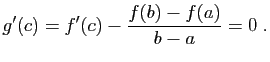
D'où le résultat. Graphiquement, le théorème des accroissements finis dit que la courbe représentative de
Graphiquement, le théorème des accroissements finis dit que la courbe représentative de  sur
sur ![$ [a,b]$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img193.gif) possède au moins une tangente parallèle à la sécante passant par
possède au moins une tangente parallèle à la sécante passant par 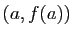 et
et 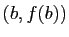 (figure 5). Si
(figure 5). Si 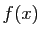 représente la position d'un mobile à l'instant
représente la position d'un mobile à l'instant  , le théorème des accroissements finis dit que en au moins un point, la vitesse instantanée doit être égale à la vitesse moyenne sur l'intervalle.
, le théorème des accroissements finis dit que en au moins un point, la vitesse instantanée doit être égale à la vitesse moyenne sur l'intervalle.
Le plus souvent en pratique, on ne sait rien de la valeur de 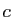 qui est telle que la tangente en
qui est telle que la tangente en 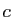 est parallèle à la sécante. Mais de son existence découlent des inégalités permettant d'obtenir des renseignements précis sur les accroissements de la fonction. Le théorème des accroissements finis permet aussi d'établir le lien entre le sens de variation de
est parallèle à la sécante. Mais de son existence découlent des inégalités permettant d'obtenir des renseignements précis sur les accroissements de la fonction. Le théorème des accroissements finis permet aussi d'établir le lien entre le sens de variation de  et le signe de sa dérivée.
et le signe de sa dérivée.
Proposition 6 Soit  un intervalle ouvert non vide, et
un intervalle ouvert non vide, et  une fonction dérivable sur
une fonction dérivable sur  . La fonction
. La fonction  est :
est :
- croissante sur
 si et seulement si
si et seulement si 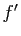 est positive ou nulle sur
est positive ou nulle sur  ,
, 
- décroissante sur
 si et seulement si
si et seulement si 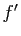 est négative ou nulle sur
est négative ou nulle sur  .
.
Démonstration : La fonction  est croissante si et seulement si
est croissante si et seulement si 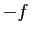 est décroissante. Il suffit donc de démontrer le premier point. Si
est décroissante. Il suffit donc de démontrer le premier point. Si  est croissante, alors ses taux d'accroissement sont tous positifs ou nuls :
est croissante, alors ses taux d'accroissement sont tous positifs ou nuls :
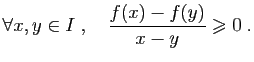
Comme la dérivée en chaque point est limite de taux d'accroissement, elle est aussi positive ou nulle.
Réciproquement, soient  et
et 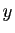 deux points de
deux points de  tels que
tels que 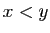 . Appliquons le théorème des accroissements finis à
. Appliquons le théorème des accroissements finis à  sur l'intervalle
sur l'intervalle ![$ [x,y]$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img221.gif) : il existe
: il existe ![$ c\in ]x,y[$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img222.gif) tel que :
tel que :
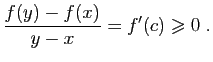
Donc 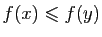 .
. Ce résultat n'est valable que sur un intervalle : la fonction
Ce résultat n'est valable que sur un intervalle : la fonction 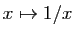 a une dérivée négative sur
a une dérivée négative sur  , pourtant elle n'est pas décroissante. D'autre part, si la dérivée est strictement positive, alors la fonction est strictement croissante. La réciproque est fausse. La fonction peut être strictement croissante même si la dérivée s'annule en certains points (par exemple
, pourtant elle n'est pas décroissante. D'autre part, si la dérivée est strictement positive, alors la fonction est strictement croissante. La réciproque est fausse. La fonction peut être strictement croissante même si la dérivée s'annule en certains points (par exemple 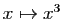 ). Comme autre application du théorème des accroissements finis, il est possible d'obtenir la dérivée en un point comme prolongement par continuité de la dérivée calculée sur un intervalle.
). Comme autre application du théorème des accroissements finis, il est possible d'obtenir la dérivée en un point comme prolongement par continuité de la dérivée calculée sur un intervalle.
Proposition 7 Soient  et
et 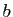 deux réels tels que
deux réels tels que 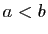 . Soit
. Soit  une fonction de
une fonction de  dans
dans  , continue sur l'intervalle
, continue sur l'intervalle ![$ [a,b]$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img193.gif) , dérivable sur
, dérivable sur ![$ ]a,b[ $](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img194.gif) . Si
. Si 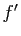 admet une limite finie en
admet une limite finie en  , alors
, alors  est dérivable à droite en
est dérivable à droite en  et :
et :
Démonstration : Soit ![$ x\in ]a,b]$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img228.gif) . Appliquons le théorème des accroissements finis sur l'intervalle
. Appliquons le théorème des accroissements finis sur l'intervalle ![$ [a,x]$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img21.gif) . Il existe
. Il existe ![$ c\in ]a,x[$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img229.gif) tel que
tel que
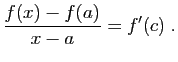
Soit  la limite à droite de
la limite à droite de 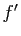 en
en  . Pour tout
. Pour tout 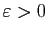 , il existe
, il existe 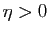 tel que
tel que
Donc pour 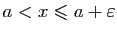 ,
,
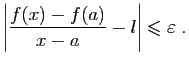
D'où le résultat. Ce résultat n'est qu'une condition suffisante. Il peut se faire que la dérivée existe sans qu'elle soit continue. Par exemple la fonction
Ce résultat n'est qu'une condition suffisante. Il peut se faire que la dérivée existe sans qu'elle soit continue. Par exemple la fonction 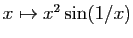 a une dérivée nulle en 0 (figure 3). Pourtant sa dérivée en
a une dérivée nulle en 0 (figure 3). Pourtant sa dérivée en  ,
, 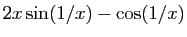 , n'a pas de limite en 0.
, n'a pas de limite en 0.
Fonctions convexes
Définition 7 Soit  une fonction de
une fonction de  dans
dans  , définie sur un intervalle
, définie sur un intervalle  contenant au moins deux points. On dit que
contenant au moins deux points. On dit que  est convexe sur
est convexe sur  si et seulement si :
si et seulement si :
| (2) |
Si 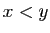 , et
, et ![$ \lambda\in[0,1]$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img239.gif) , alors
, alors 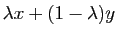 est un point de l'intervalle
est un point de l'intervalle ![$ [x,y]$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img221.gif) . La condition (2) dit que le point de la courbe représentative d'abscisse
. La condition (2) dit que le point de la courbe représentative d'abscisse 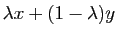 doit être situé au-dessous du segment de sécante joignant les points
doit être situé au-dessous du segment de sécante joignant les points 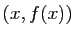 et
et 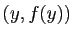 (figure 6). En d'autres termes, tout arc de la courbe représentative doit être situé au-dessous de sa corde. De manière équivalente, la partie du plan située au-dessus de la courbe représentative est une région convexe, au sens où tout segment joignant deux de ses points est entièrement contenu dans la région.
(figure 6). En d'autres termes, tout arc de la courbe représentative doit être situé au-dessous de sa corde. De manière équivalente, la partie du plan située au-dessus de la courbe représentative est une région convexe, au sens où tout segment joignant deux de ses points est entièrement contenu dans la région.
![\includegraphics[width=8cm]{convexe}](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img242.gif) |
Une fonction est dite concave si son opposée est convexe. Les propriétés sont inversées : tout arc est au-dessus de sa corde. La région du plan située au-dessous de la courbe représentative est convexe.
La fonction exponentielle est convexe, la fonction logarithme est concave. La fonction 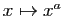 est convexe sur
est convexe sur  pour
pour 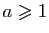 , elle est concave pour
, elle est concave pour 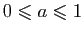 . La fonction
. La fonction 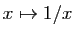 est convexe sur
est convexe sur 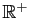 , concave sur
, concave sur 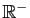 , de même que la fonction
, de même que la fonction 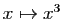 . Voici une autre caractérisation de la convexité.
. Voici une autre caractérisation de la convexité.
Proposition 8 Soit  une fonction de
une fonction de  dans
dans  , définie sur un intervalle
, définie sur un intervalle  contenant au moins deux points. La fonction
contenant au moins deux points. La fonction  est convexe sur
est convexe sur  si et seulement si, pour tout
si et seulement si, pour tout 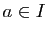 le taux d'accroissement
le taux d'accroissement 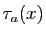 est une fonction croissante de
est une fonction croissante de  sur
sur 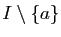 .
.
Démonstration : Commmençons par la condition nécessaire. Soit  et
et  tels que
tels que 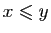 . Trois cas sont possibles :
. Trois cas sont possibles : 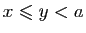 ,
, 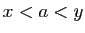 ,
,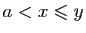 . Nous traitons le premier, les deux autres sont analogues. Soit
. Nous traitons le premier, les deux autres sont analogues. Soit 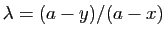 . Alors
. Alors 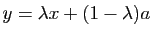 . Comme
. Comme  est convexe,
est convexe,
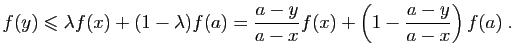
On en déduit :
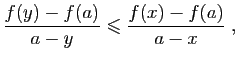
soit :
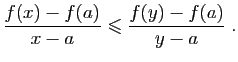
Montrons maintenant la condition suffisante. Soient  et
et 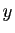 deux points de
deux points de  tels que
tels que 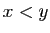 et
et 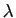 un réel dans
un réel dans ![$ [0,1]$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img261.gif) . Posons
. Posons 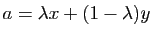 , et donc :
, et donc :
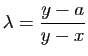 et
et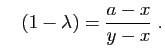
Si 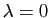 ou
ou 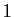 , l'inégalité est vérifiée. Nous pouvons donc supposer que
, l'inégalité est vérifiée. Nous pouvons donc supposer que  est différent de
est différent de  et
et 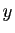 . Écrivons que le taux d'accroissement en
. Écrivons que le taux d'accroissement en  est croissant.
est croissant.
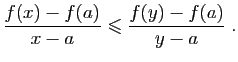
En multipliant les deux membres par le produit 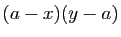 , qui est positif, on obtient :
, qui est positif, on obtient :
En divisant par 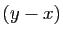 ceci donne :
ceci donne :
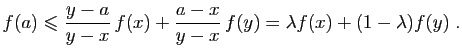
- Corollaire 1 Si une fonction
 est convexe sur un intervalle ouvert
est convexe sur un intervalle ouvert  , alors elle est dérivable à gauche et à droite en tout point de
, alors elle est dérivable à gauche et à droite en tout point de  , et donc continue sur
, et donc continue sur  .
. - Démonstration : Si
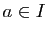 , le taux d'accroissement en
, le taux d'accroissement en  ,
, 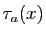 , est une fonction croissante de
, est une fonction croissante de  . Il admet donc en
. Il admet donc en  une limite à gauche et une limite à droite finies.
une limite à gauche et une limite à droite finies. Ce résultat n'est pas valable si l'intervalle n'est pas ouvert. Par exemple la fonction qui vaut 0 sur
Ce résultat n'est pas valable si l'intervalle n'est pas ouvert. Par exemple la fonction qui vaut 0 sur 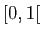 , et
, et 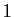 au point
au point 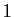 est convexe sur
est convexe sur ![$ [0,1]$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img261.gif) , mais elle n'est pas continue en
, mais elle n'est pas continue en  . Le fait qu'une dérivée à gauche et à droite existe, n'implique pas que la fonction soit dérivable. Par exemple, la fonction valeur absolue
. Le fait qu'une dérivée à gauche et à droite existe, n'implique pas que la fonction soit dérivable. Par exemple, la fonction valeur absolue 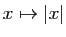 est convexe sur
est convexe sur  mais elle n'est pas dérivable en 0. Lorsque la fonction est dérivable, sa dérivée est croissante.
mais elle n'est pas dérivable en 0. Lorsque la fonction est dérivable, sa dérivée est croissante. - Proposition 9 Soit
 une fonction de
une fonction de  dans
dans  , dérivable sur un intervalle ouvert
, dérivable sur un intervalle ouvert  . La fonction
. La fonction  est convexe sur
est convexe sur  si et seulement si sa dérivée
si et seulement si sa dérivée 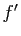 est croissantesur
est croissantesur  .
. - Démonstration : Commençons par la condition nécessaire. Soient
 et
et 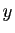 deux points de
deux points de  , tels que
, tels que 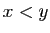 . Pour tout
. Pour tout ![$ z\in [x,y]$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img272.gif) ,
,
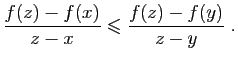
En faisant tendre 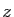 vers
vers  , on en déduit :
, on en déduit :
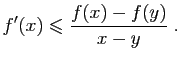
De même, en faisant tendre 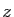 vers
vers 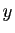 ,
,
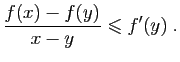
Donc 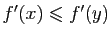 .
.
Montrons maintenant la condition suffisante. Soient  deux points de
deux points de  tels que
tels que 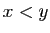 ,
, ![$ \lambda\in ]0,1[ $](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img279.gif) , et
, et 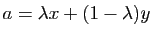 . Appliquons le théorème des accroissements finis sur les deux intervalles
. Appliquons le théorème des accroissements finis sur les deux intervalles ![$ [x,a]$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img280.gif) et
et ![$ [a,y]$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img281.gif) . Il existe
. Il existe ![$ c_1\in ]x,a[$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img282.gif) et
et ![$ c_2\in ]a,y[$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img283.gif) tels que :
tels que :
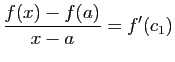 et
et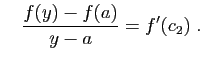
La fonction 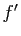 étant croissante, on a donc :
étant croissante, on a donc :
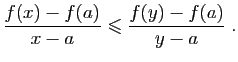
Comme nous l'avons déjà vu dans la démonstration de la proposition 8, ceci entraîne
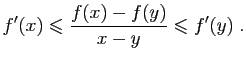
On en déduit que pour 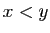 ,
,
Donc la courbe représentative de  reste au-dessus de ses tangentes (figure 6).
reste au-dessus de ses tangentes (figure 6).
Corollaire 2 Soit  une fonction de
une fonction de  dans
dans  , deux fois dérivable sur un intervalle ouvert
, deux fois dérivable sur un intervalle ouvert  . La fonction
. La fonction  est convexe sur
est convexe sur  si et seulement si sa dérivée seconde
si et seulement si sa dérivée seconde 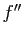 est positive ou nulle sur
est positive ou nulle sur  .
.
Une fonction deux fois dérivable est concave si et seulement si sa dérivée seconde est négative ou nulle. Les points où la dérivée seconde s'annule et change de signe correspondent graphiquement à des points où la courbe représentative passe de concave à convexe où inversement. On les appelle des points d'inflexion.
Exercices
- Exercice 1 Pour chacune des fonctions
 définies ci-dessous :
définies ci-dessous :
- Donner une expression explicite du taux d'accroissement de
 en un point
en un point  quelconque du domaine de définition.
quelconque du domaine de définition. - Calculer la limite en
 de ce taux d'accroissement et retrouver l'expression de la dérivée de
de ce taux d'accroissement et retrouver l'expression de la dérivée de  en
en  .
.
- Exercice 2 Soient
 et
et  deux fonctions définies sur un intervalle ouvert
deux fonctions définies sur un intervalle ouvert  . On suppose que
. On suppose que  et
et  sont dérivables en
sont dérivables en 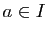 et que
et que 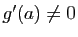 . Montrer que :
. Montrer que :
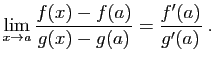
(C'est la «Règle de l'Hôpital»).
- Exercice 3 Pour chacune des applications
 définies ci-dessous :
définies ci-dessous :
- Verifiez que
 est prolongeable par continuité en 0.
est prolongeable par continuité en 0. - L'application prolongée est-elle dérivable en 0 ?
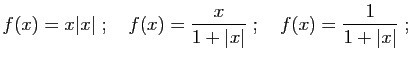
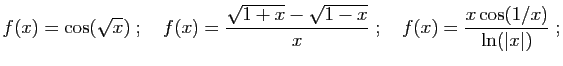
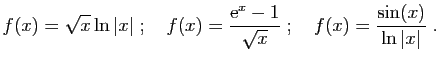
- Exercice 4 Pour chacune des fonctions
 définies ci-dessous :
définies ci-dessous :
- Préciser le domaine de définition de
 .
. - Soit
 un intervalle ouvert inclus dans
un intervalle ouvert inclus dans  . Démontrer que
. Démontrer que  est dérivable sur
est dérivable sur  .
. - Calculer l'expression de la dérivée de
 .
.
![$\displaystyle f(x)= (x(x-2))^{1/3}
\;;\quad
f(x)= \frac{1}{\sqrt[3]{x^2}}-\frac{1}{\sqrt{x^3}}
\;;\quad
f(x)= \sqrt{x+\sqrt{1+x^2}}\;;
$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img312.gif)
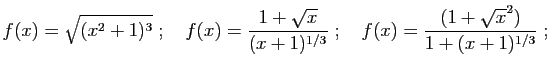
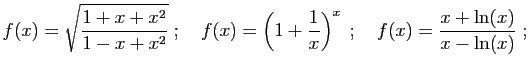
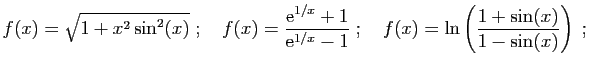
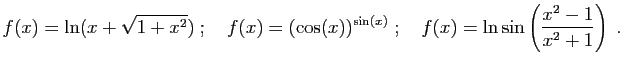
- Exercice 5 Pour chacune des fonctions
 définies ci-dessous, sur un intervalle
définies ci-dessous, sur un intervalle ![$ [a,b]$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img193.gif) :
:
- Démontrer que
 est dérivable sur
est dérivable sur ![$ ]a,b[ $](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img194.gif) .
. - La fonction
 est-elle dérivable à droite en
est-elle dérivable à droite en  ?
? - La fonction
 est-elle dérivable à gauche en
est-elle dérivable à gauche en 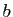 ?
?
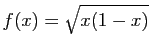 sur
sur ![$\displaystyle [0,1]
\;;\quad
f(x)=\sqrt{(1-x^2)(1-x)}$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img318.gif) sur
sur 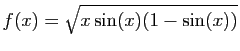 sur
sur 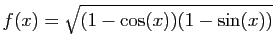 sur
sur
Exercice 6 Pour tout 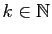 , calculer la dérivée d'ordre
, calculer la dérivée d'ordre 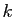 des fonctions suivantes.
des fonctions suivantes.
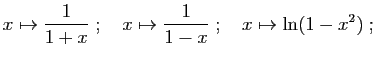
Exercice 7
- Déterminer les réels
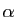 et
et 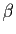 tels que la fonction
tels que la fonction  définie ci-dessous soit de classe
définie ci-dessous soit de classe 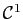 sur
sur  .
.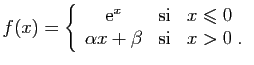
- Déterminer les réels
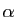 ,
, 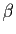 et
et 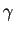 tels que la fonction
tels que la fonction  définie ci-dessous soit de classe
définie ci-dessous soit de classe 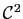 sur
sur  .
.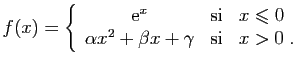
- Déterminer les réels
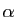 et
et 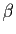 tels que la fonction
tels que la fonction  définie ci-dessous soit de classe
définie ci-dessous soit de classe 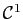 sur
sur ![$ ]0,+\infty[ $](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img335.gif) .
.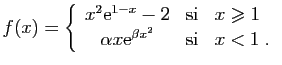
Exercice 8 On dit qu'une fonction de  dans
dans  est paire si pour tout
est paire si pour tout 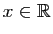 ,
, 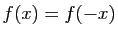 . On dit qu'elle est est impaire si pour tout
. On dit qu'elle est est impaire si pour tout 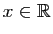 ,
, 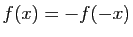 . Soit
. Soit  une fonction dérivable sur
une fonction dérivable sur  .
.
- Montrer que si
 est paire alors
est paire alors 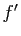 est impaire.
est impaire. - Montrer que si
 est impaire alors
est impaire alors 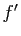 est paire.
est paire.
Exercice 9 Soit  la fonction de
la fonction de  dans
dans  définie par
définie par 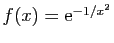 si
si 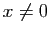 et
et 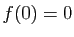 .
.
- Montrer que pour tout
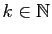 ,
, 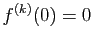 .
. - Soit
 la fonction de
la fonction de  dans
dans  définie par
définie par 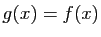 si
si 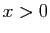 et
et 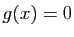 si
si 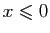 . Montrer que
. Montrer que  est de classe
est de classe 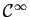 sur
sur  .
. - Soient
 et
et 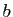 deux réels tels que
deux réels tels que 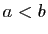 . Soit
. Soit 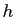 la fonction de
la fonction de  dans
dans  définie par :
définie par :![\begin{displaymath}
h(x)=\left\{
\begin{array}{ccl}
f(x-a)&\mbox{si}&x< a\\
0&\...
...{si}&x\in[a,b]\\
f(x-b)&\mbox{si}& x> b\;.
\end{array}\right.
\end{displaymath}](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img347.gif) Montrer que
Montrer que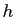 est de classe
est de classe 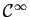 sur
sur  . Représenter graphiquement
. Représenter graphiquement 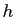 pour
pour 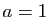 et
et 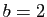 .
.
Exercice 10 Soient  et
et 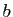 deux réels tels que
deux réels tels que 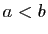 . Soit
. Soit  une fonction définie sur
une fonction définie sur ![$ [a,b]$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img193.gif) , dérivable à gauche et à droite en tout point de
, dérivable à gauche et à droite en tout point de ![$ ]a,b[ $](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img194.gif) . On suppose que
. On suppose que  est continue à gauche en
est continue à gauche en  , à droite en
, à droite en 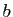 et que
et que 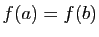 . Montrer qu'il existe un point
. Montrer qu'il existe un point ![$ c\in ]a,b[$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img349.gif) tel que le produit de la dérivée à gauche en
tel que le produit de la dérivée à gauche en 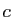 par la dérivée à droite en
par la dérivée à droite en 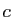 soit négatif ou nul.
soit négatif ou nul.
Exercice 11 Soit  une fonction continue sur
une fonction continue sur 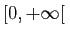 , dérivable sur
, dérivable sur ![$ ]0,+\infty[ $](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img335.gif) , telle que
, telle que
Montrer qu'il existe 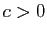 tel que
tel que 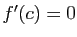 .
.
Exercice 12 Soient  et
et 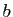 deux réels tels que
deux réels tels que 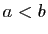 . Soient
. Soient  et
et  deux fonctions définies sur
deux fonctions définies sur ![$ [a,b]$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img193.gif) , dérivables sur
, dérivables sur ![$ ]a,b[ $](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img194.gif) . On suppose que
. On suppose que 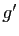 ne s'annule pas sur
ne s'annule pas sur ![$ ]a,b[ $](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img194.gif) .
.
- Montrer que le théorème de Rolle s'applique à la fonction
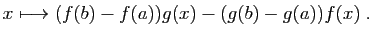
- En déduire qu'il existe un point
![$ c\in ]a,b[$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img349.gif) tel que :
tel que :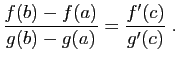
Exercice 13 Soit  une fonction continue sur
une fonction continue sur 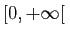 , dérivable sur
, dérivable sur ![$ ]0,+\infty[ $](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img335.gif) , telle que
, telle que 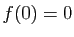 . On suppose que
. On suppose que 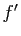 est croissante sur
est croissante sur ![$ ]0,+\infty[ $](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img335.gif) . Démontrer que la fonction
. Démontrer que la fonction  définie sur
définie sur ![$ ]0,+\infty[$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img357.gif) par
par 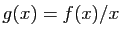 est croissante.
est croissante.
Exercice 14
- Etudier les variations de la fonction
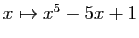 sur
sur  . En déduire que l'équation
. En déduire que l'équation 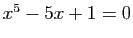 a trois solutions réelles.
a trois solutions réelles. - Soient
 et
et 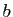 deux réels et
deux réels et  un entier naturel. Montrer que l'équation
un entier naturel. Montrer que l'équation 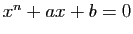 a au plus trois solutions réelles.
a au plus trois solutions réelles. - Soit
 un entier naturel supérieur ou égal à
un entier naturel supérieur ou égal à 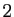 . Montrer que l'équation
. Montrer que l'équation 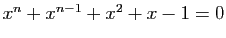 a une seule solution réelle positive.
a une seule solution réelle positive. - Soit
 un réel positif et
un réel positif et  un entier naturel pair. Montrer que l'équation
un entier naturel pair. Montrer que l'équation 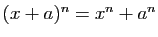 admet
admet 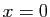 pour seule solution réelle.
pour seule solution réelle.
Exercice 15
- Soient
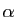 ,
, 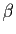 et
et 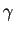 trois réels. On considère la fonction
trois réels. On considère la fonction  définie par
définie par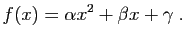 Soient
Soient et
et 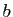 deux réels tels que
deux réels tels que 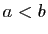 . Déterminer le point
. Déterminer le point ![$ c\in ]a,b[$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img349.gif) tel que
tel que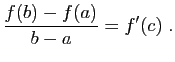
- Soient
 ,
,  et
et 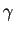 trois réels. On considère la fonction
trois réels. On considère la fonction  définie par
définie par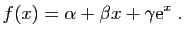 Soient
Soient et
et 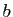 deux réels tels que
deux réels tels que 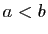 . Déterminer le point
. Déterminer le point ![$ c\in ]a,b[$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img349.gif) tel que
tel que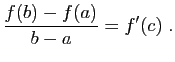
Exercice 16 Utiliser le théorème des accroissements finis pour donner un majorant des réels suivants. Comparer ce majorant avec une approximation numérique à 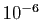 près.
près.
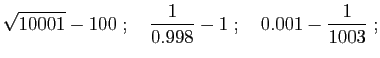
Exercice 17
- Soient
 et
et 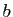 deux réels tels que
deux réels tels que 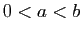 . Montrer que :
. Montrer que :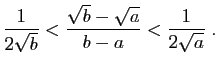
- Pour tout
 , on pose :
, on pose :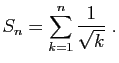 Démontrer que pour tout
Démontrer que pour tout ,
,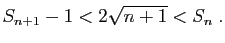
- Soient
 et
et 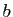 deux réels tels que
deux réels tels que 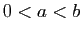 . Montrer que :
. Montrer que :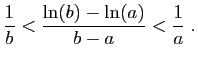
- Pour tout
 , on pose :
, on pose : Démontrer que pour tout
Démontrer que pour tout ,
,
Exercice 18
- Utiliser le théorème des accroissements finis, appliqué à la fonction exponentielle pour démontrer que :
- Utiliser le théorème des accroissements finis, appliqué à la fonction
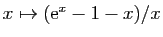 pour démontrer que :
pour démontrer que :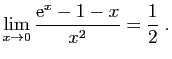
- Utiliser le théorème des accroissements finis, appliqué à la fonction logarithme pour démontrer que :
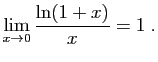
- Utiliser le théorème des accroissements finis, appliqué à la fonction
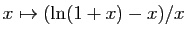 pour démontrer que :
pour démontrer que :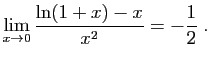
- Utiliser le théorème des accroissements finis, appliqué à la fonction cosinus pour démontrer que :
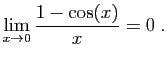
- Utiliser le théorème des accroissements finis, appliqué à la fonction
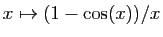 pour démontrer que :
pour démontrer que :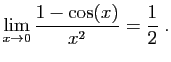
- Utiliser le théorème des accroissements finis, appliqué à la fonction
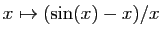 pour démontrer que :
pour démontrer que :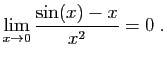
- Utiliser le théorème des accroissements finis, appliqué à la fonction
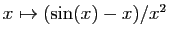 pour démontrer que :
pour démontrer que :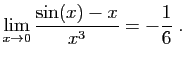
Exercice 19 Soient  et
et 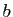 deux réels tels que
deux réels tels que 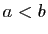 . Soit
. Soit  une fonction deux fois dérivable sur
une fonction deux fois dérivable sur ![$ [a,b]$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img193.gif) telle que
telle que 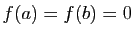 et pour tout
et pour tout ![$ x\in ]a,b[ $](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img394.gif) ,
,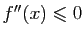 . Montrer que, pour tout
. Montrer que, pour tout ![$ x\in [a,b]$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img199.gif) ,
, 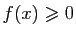 .
.
Exercice 20 Soit  une fonction deux fois dérivable sur
une fonction deux fois dérivable sur  telle que pour tout
telle que pour tout 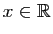 ,
, 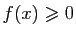 ,
, 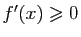 et
et 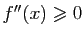 .
.
- Montrer que si
 est majorée alors
est majorée alors  est constante.
est constante. - Montrer que si
 n'est pas majorée, alors :
n'est pas majorée, alors :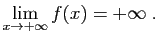
- Montrer que la limite quand
 tend vers
tend vers 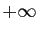 de
de 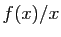 existe, et qu'elle est soit infinie, soit finie et strictement positive.
existe, et qu'elle est soit infinie, soit finie et strictement positive. - Soit
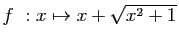 . Montrer que
. Montrer que  vérifie les hypothèses de l'exercice, et calculer la limite quand
vérifie les hypothèses de l'exercice, et calculer la limite quand  tend vers
tend vers 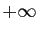 de
de 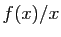 .
.
Exercice 21 Soit  une fonction convexe sur un intervalle ouvert
une fonction convexe sur un intervalle ouvert  , dérivable en un point
, dérivable en un point 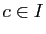 , et telle que
, et telle que 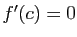 . Montrer que
. Montrer que 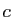 est un minimum global pour
est un minimum global pour  sur I :
sur I :
Exercice 22
- Soit
 une fonction convexe sur un intervalle
une fonction convexe sur un intervalle  . Montrer que pour tout
. Montrer que pour tout 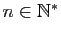 , pour tout
, pour tout 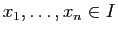 ,
,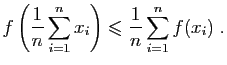
- Démontrer que pour tout
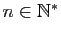 , et pour tout
, et pour tout 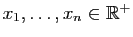 ,
,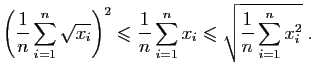
- Démontrer que pour tout
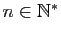 , et pour tout
, et pour tout 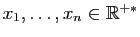 ,
,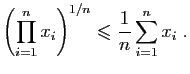
- Démontrer que pour tout
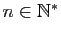 , et pour tout
, et pour tout 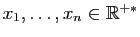 ,
,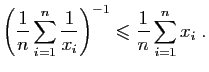
Exercice 23 Soient 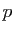 et
et 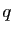 deux réels strictement positifs tels que :
deux réels strictement positifs tels que :
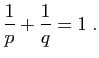
- Montrer que, pour tout
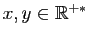 ,
,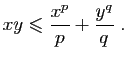
- Soient
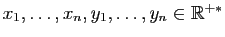 tels que :
tels que :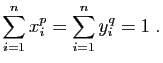 Montrer que :
Montrer que :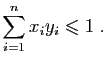
- Soient
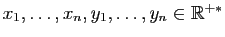 . Démontrer l'inégalité de Hölder :
. Démontrer l'inégalité de Hölder :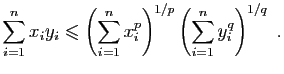
- Soit
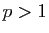 . Démontrer l'inégalité de Minkowski :
. Démontrer l'inégalité de Minkowski :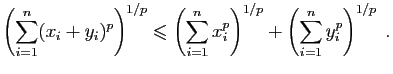 (On posera
(On posera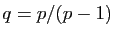 et
et 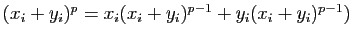 .
.
QCM
Donnez-vous une heure pour répondre à ce questionnaire. Les 10 questions sont indépendantes. Pour chaque question 5 affirmations sont proposées, parmi lesquelles 2 sont vraies et 3 sont fausses. Pour chaque question, cochez les 2 affirmations que vous pensez vraies. Chaque question pour laquelle les 2 affirmations vraies sont cochées rapporte 2 points.
Question 1 Soit  la fonction
la fonction 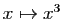 et
et 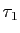 le taux d'accroissement de
le taux d'accroissement de  au point
au point  .
.
- Le taux d'accroissement
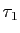 est une fonction de
est une fonction de 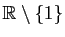 dans
dans  .
. 
- Le taux d'accroissement
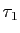 est égal à
est égal à 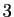 .
. 
- Pour tout
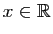 ,
,  .
. 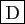
- Le taux d'accroissement
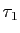 n'admet pas de limite quand
n'admet pas de limite quand  tend vers
tend vers 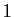 .
. 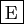
- Le taux d'accroissement
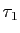 est prolongeable par continuité en
est prolongeable par continuité en  .
.
Question 2 Soit  une fonction définie sur
une fonction définie sur  ,
, 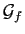 son graphe, et
son graphe, et  un point de
un point de  .
.
- Si
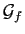 admet une tangente au point
admet une tangente au point  , alors
, alors  est dérivable en
est dérivable en  .
. 
- Si
 n'est pas dérivable en
n'est pas dérivable en  , alors
, alors  n'est pas continue en
n'est pas continue en  .
. 
- Si
 est dérivable en
est dérivable en  , alors au voisinage de
, alors au voisinage de 
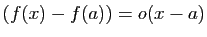 .
. 
- Si
 admet une dérivée nulle en
admet une dérivée nulle en  , alors
, alors  admet une tangente horizontale au point
admet une tangente horizontale au point  .
. 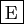
- Si le taux d'accroissement de
 en
en  tend vers
tend vers 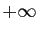 quand
quand  tend vers
tend vers  , alors
, alors 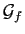 admet une tangente verticale au point
admet une tangente verticale au point 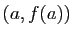 .
.
Question 3 Soit  la fonction définie par
la fonction définie par 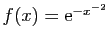 si
si 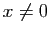 et
et 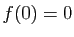 .
.
- La dérivée de
 en 0 est nulle.
en 0 est nulle. 
- La dérivée de
 en
en  est
est  .
. 
- Le graphe de
 admet une tangente verticale en 0.
admet une tangente verticale en 0. 
- La dérivée de
 en
en 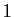 est
est 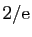 .
. 
- Pour tout
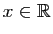 les dérivées de
les dérivées de  en
en  et en
et en 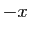 sont égales.
sont égales.
Question 4 Soit  la fonction qui à
la fonction qui à ![$ x\in[-1,1]$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img440.gif) associe
associe 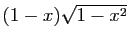 .
.
- La fonction
 est indéfiniment dérivable sur
est indéfiniment dérivable sur ![$ ]-1,1[ $](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img442.gif) .
. 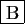
- La fonction
 est dérivable à droite en
est dérivable à droite en 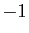 .
. 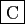
- Le graphe de
 admet une tangente verticale en
admet une tangente verticale en 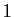 .
. 
- La dérivée de
 en 0 est nulle.
en 0 est nulle. 
- La dérivée et la dérivée seconde de
 prennent la même valeur en 0.
prennent la même valeur en 0.
Question 5 Soit 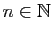 un entier.
un entier.
- La dérivée
 -ième de
-ième de 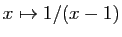 est
est  .
. 
- La dérivée seconde de
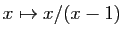 s'annule en 0.
s'annule en 0. 
- La dérivée troisième de
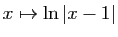 est
est 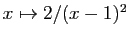 .
. 
- La dérivée seconde de
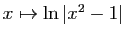 est
est 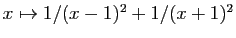 .
. 
- La dérivée troisième de
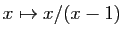 est
est 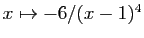 .
.
Question 6 Soit  une fonction dérivable de
une fonction dérivable de  dans
dans  . Soient
. Soient  et
et 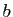 deux réels.
deux réels.
- Si
 présente un maximum local en
présente un maximum local en  , alors
, alors 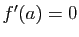 .
. 
- Si
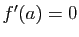 , alors
, alors  présente un extremum local en
présente un extremum local en  .
. 
- Si
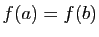 , alors
, alors  atteint son maximum sur
atteint son maximum sur ![$ [a,b]$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img193.gif) .
. 
- Si
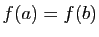 , alors
, alors  présente un extremum local en un point de
présente un extremum local en un point de ![$ ]a,b[ $](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img194.gif) .
. 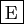
- S'il existe
![$ c\in ]a,b[$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img349.gif) tel que
tel que 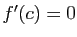 , alors
, alors 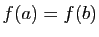 .
.
Question 7 Soit  une fonction de
une fonction de ![$ [0,1]$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img261.gif) dans
dans  , continue sur
, continue sur ![$ [0,1]$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img261.gif) et dérivable sur
et dérivable sur ![$ ]0,1[ $](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img451.gif) . On suppose que
. On suppose que 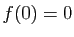 et
et 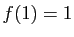 .
.
- La fonction
 est croissante sur
est croissante sur ![$ [0,1]$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img261.gif) .
. 
- Il existe
![$ c\in ]0,1[$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img453.gif) tel que
tel que 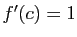 .
. 
- Pour tout
![$ c\in ]0,1[ $](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img454.gif) ,
, 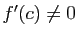 .
. 
- La fonction
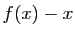 admet un extremum local sur
admet un extremum local sur ![$ ]0,1[ $](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img451.gif) .
. 
- La fonction
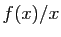 admet un extremum local sur
admet un extremum local sur ![$ ]0,1[ $](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img451.gif) .
.
Question 8 Soit  une fonction dérivable de
une fonction dérivable de  dans
dans  .
.
- Si
 est strictement décroissante sur
est strictement décroissante sur  , alors
, alors 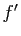 est strictement négative sur
est strictement négative sur  .
. 
- Si
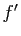 est négative ou nulle sur
est négative ou nulle sur  , alors
, alors  est décroissante sur
est décroissante sur  .
. 
- Si
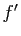 est strictement négative sur
est strictement négative sur  , alors
, alors  est strictement décroissante sur
est strictement décroissante sur  .
. 
- Si
 est décroissante sur
est décroissante sur  , alors
, alors 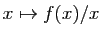 est décroissante sur
est décroissante sur 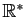 .
. 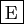
- Si
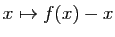 est décroissante sur
est décroissante sur  , alors
, alors  est décroissante sur
est décroissante sur  .
.
Question 9 Soit  une fonction de
une fonction de ![$ [0,1]$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img261.gif) dans
dans  .
.
- Si
 est convexe sur
est convexe sur ![$ ]0,1[$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img459.gif) alors
alors  est continue sur
est continue sur ![$ ]0,1[ $](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img451.gif) .
. 
- Si pour tout
![$ \lambda\in ]0,1[ $](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img460.gif) ,
, 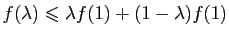 , alors
, alors  est convexe sur
est convexe sur ![$ [0,1]$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img261.gif) .
. 
- Si
 est convexe sur
est convexe sur ![$ [0,1]$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img261.gif) et
et 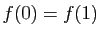 , alors il existe
, alors il existe ![$ c\in ]0,1[$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img453.gif) tel que la dérivée de
tel que la dérivée de  en
en  existe et soit nulle.
existe et soit nulle. 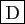
- Si
 est dérivable en un point
est dérivable en un point 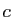 de
de ![$ ]0,1[ $](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img451.gif) , alors
, alors 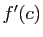 est inférieure à
est inférieure à 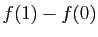 .
. 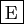
- Si
 est convexe sur
est convexe sur ![$ [0,1]$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img261.gif) et
et 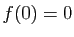 , alors la fonction
, alors la fonction 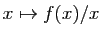 est croissante sur
est croissante sur ![$ ]0,1[ $](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img451.gif) .
.
Question 10 Soit  la fonction de
la fonction de  dans
dans  , qui à
, qui à  associe
associe 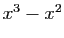 .
.
- La fonction
 est croissante sur
est croissante sur 
- La fonction
 présente un maximum local en 0.
présente un maximum local en 0. 
- La fonction
 présente un minimum global en
présente un minimum global en  .
. 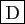
- La fonction
 est convexe sur
est convexe sur 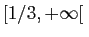 .
. 
- La fonction
 est croissante sur
est croissante sur 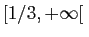 .
.
Devoir
Essayez de bien rédiger vos réponses, sans vous reporter ni au cours, ni au corrigé. Si vous souhaitez vous évaluer, donnez-vous deux heures ; puis comparez vos réponses avec le corrigé et comptez un point pour chaque question à laquelle vous aurez correctement répondu.
Questions de cours : Soit  une fonction définie sur
une fonction définie sur  , à valeurs dans
, à valeurs dans  . Soit
. Soit  un point de
un point de  .
.
- Qu'appelle-t-on taux d'accroissement de
 en
en  ?
? - Quand dit-on que la fonction
 est dérivable en
est dérivable en  ?
? - Démontrer que
 est dérivable en
est dérivable en  si et seulement si, au voisinage de 0 :
si et seulement si, au voisinage de 0 :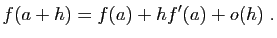
- Quand dit-on que
 est convexe sur
est convexe sur  ?
? - Si
 est convexe sur
est convexe sur  , que peut-on dire du taux d'accroissement de
, que peut-on dire du taux d'accroissement de  en
en  ? Que peut-on dire de la dérivée de
? Que peut-on dire de la dérivée de  en
en  ?
?
Exercice 1 : On admettra dans cet exercice les limites suivantes.
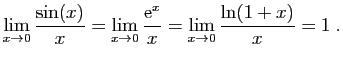
- Démontrer que :
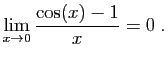
- Soit
 un réel quelconque. Démontrer que la fonction
un réel quelconque. Démontrer que la fonction 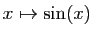 est dérivable en
est dérivable en  , et que sa dérivée est
, et que sa dérivée est 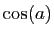 .
. - Soit
 un réel quelconque. Démontrer que la fonction
un réel quelconque. Démontrer que la fonction 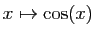 est dérivable en
est dérivable en  , et que sa dérivée est
, et que sa dérivée est 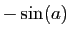 .
. - Soit
 un réel quelconque. Démontrer que la fonction
un réel quelconque. Démontrer que la fonction 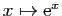 est dérivable en
est dérivable en  , et que sa dérivée est
, et que sa dérivée est 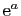 .
. - Soit
 un réel strictement positif. Démontrer que la fonction
un réel strictement positif. Démontrer que la fonction 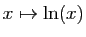 est dérivable en
est dérivable en  , et que sa dérivée est
, et que sa dérivée est 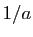 .
.
Exercice 2 : Soit  la fonction de
la fonction de  dans
dans  qui à
qui à  associe :
associe :
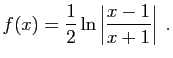
- Déterminer le domaine de définition de
 , noté
, noté 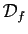 . Montrer que
. Montrer que  est dérivable sur
est dérivable sur 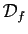 et calculer sa dérivée. Montrer que
et calculer sa dérivée. Montrer que  est strictement croissante sur
est strictement croissante sur![$ ]-\infty,-1[$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img480.gif) et sur
et sur ![$ ]1,+\infty[ $](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img481.gif) , strictement décroissante sur
, strictement décroissante sur ![$ ]-1,1[ $](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img442.gif) .
. - Calculer la dérivée seconde de
 . Montrer que
. Montrer que  est convexe sur
est convexe sur ![$ ]-\infty,-1[$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img480.gif) et sur
et sur ![$ ]-1,0] $](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img482.gif) , concave sur
, concave sur 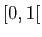 et sur
et sur ![$ ]1,+\infty[ $](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img481.gif) .
. - Soit
 un réel. Soit
un réel. Soit 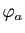 la fonction qui à
la fonction qui à 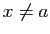 associe
associe 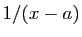 . Démontrer que la dérivée
. Démontrer que la dérivée  -ième de
-ième de 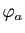 est la fonction définie par :
est la fonction définie par :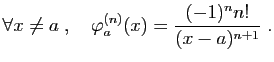
- En déduire la dérivée
 -ième de
-ième de  , pour tout entier
, pour tout entier 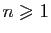 .
. - Pour tout
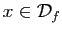 , on pose
, on pose 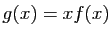 . Calculer la dérivée seconde de
. Calculer la dérivée seconde de  . En déduire que
. En déduire que  est concave sur tout intervalle inclus dans
est concave sur tout intervalle inclus dans 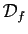 .
. - Montrer que
 admet un maximum global en 0. Vérifier que
admet un maximum global en 0. Vérifier que 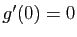 et
et 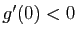 .
. - Pour tout entier
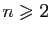 , donner l'expression de la dérivée
, donner l'expression de la dérivée  -ième de
-ième de  en fonction de
en fonction de  .
.
Exercice 3 : Soit  une fonction de
une fonction de ![$ ]0,+\infty[$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img357.gif) dans
dans  , dérivable sur
, dérivable sur ![$ ]0,+\infty[ $](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img335.gif) .
.
- On suppose que
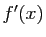 tend vers 0 quand
tend vers 0 quand  tend vers
tend vers 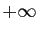 . Montrer que :
. Montrer que :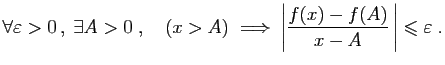
- En déduire que :
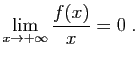
- Soit
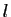 un réel. On suppose que
un réel. On suppose que 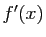 tend vers
tend vers 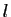 quand
quand  tend vers
tend vers 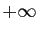 . Montrer que :
. Montrer que :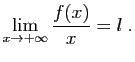 (Indication : considérer la fonction
(Indication : considérer la fonction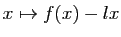 ).
).
Corrigé du devoir
Questions de cours :
- Le taux d'accroissement de
 en
en  est l'application notée
est l'application notée 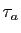 , qui à
, qui à 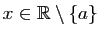 associe :
associe :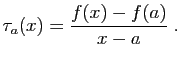
- On dit que
 est dérivable en
est dérivable en  si le taux d'accroissement de
si le taux d'accroissement de  en
en  admet une limite finie en
admet une limite finie en  . Cette limite est la dérivée de
. Cette limite est la dérivée de  en
en  .
.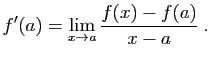
- Le taux d'accroissement
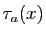 admet
admet 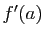 pour limite en
pour limite en  si et seulement si :
si et seulement si :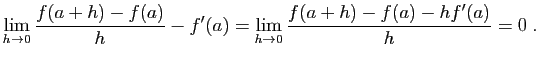 Par définition, ceci équivaut à dire que
Par définition, ceci équivaut à dire que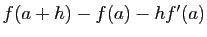 est négligeable devant
est négligeable devant 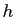 , au voisinage de 0 :
, au voisinage de 0 :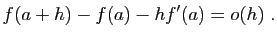
- On dit que
 est convexe sur
est convexe sur  si :
si :![$\displaystyle \forall x,y\in\mathbb{R} ,\;\forall \lambda\in[0,1]\;,\quad
f(\lambda x+(1-\lambda) y)\leqslant\lambda f(x)+(1-\lambda)f(y)\;.
$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img501.gif)
- Si
 est convexe sur
est convexe sur  , alors le taux d'accroissement de
, alors le taux d'accroissement de  en
en  est une fonction croissante sur
est une fonction croissante sur  . Comme une fonction croissante admet une limite à gauche et à droite en tout point, la dérivée à gauche et la dérivée à droite de
. Comme une fonction croissante admet une limite à gauche et à droite en tout point, la dérivée à gauche et la dérivée à droite de  en
en  existent. Mais elles ne sont pas forcément égales et
existent. Mais elles ne sont pas forcément égales et  n'est pas forcément dérivable en
n'est pas forcément dérivable en  .
.
Exercice 1 :
- Exprimons
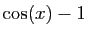 à l'aide de
à l'aide de 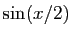 .
.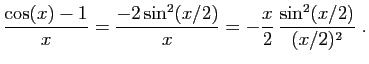 Or :
Or :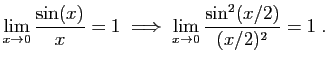 Donc :
Donc :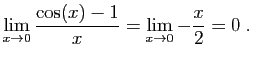
- Écrivons le taux d'accroissement en
 , évalué en
, évalué en 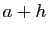 :
: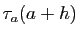
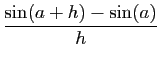
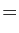
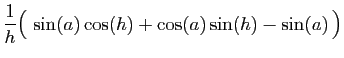
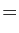
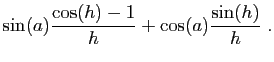 On sait que :
On sait que :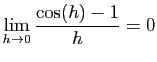 et
et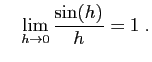 Donc :
Donc :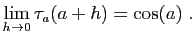
- Écrivons le taux d'accroissement en
 , évalué en
, évalué en 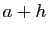 :
: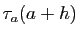
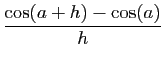
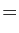
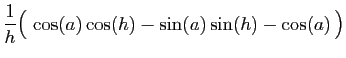
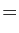
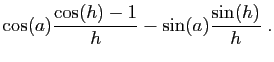 On en déduit :
On en déduit :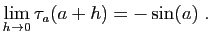
- Écrivons le taux d'accroissement en
 , évalué en
, évalué en 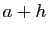 :
: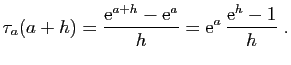 On sait que :
On sait que :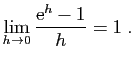 Donc :
Donc :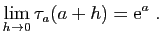
- Écrivons le taux d'accroissement en
 , évalué en
, évalué en 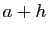 :
: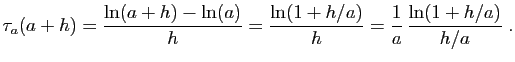 On sait que :
On sait que :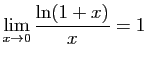 donc
donc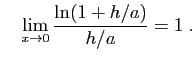 Donc :
Donc :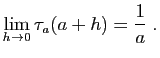
Exercice 2 :
- Exprimons
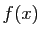 sous la forme :
sous la forme : La fonction
La fonction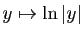 est définie pour tout
est définie pour tout 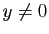 , donc
, donc 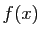 est défini pour tout
est défini pour tout  différent de
différent de 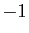 et de
et de 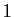 .
. La fonction
La fonction est dérivable pour tout
est dérivable pour tout  et sa dérivée est
et sa dérivée est 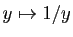 . Les fonctions
. Les fonctions 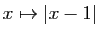 et
et 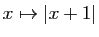 sont dérivables respectivement sur
sont dérivables respectivement sur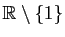 et
et  (comme fonctions polynômes). Donc
(comme fonctions polynômes). Donc  est dérivable, comme combinaison linéaire de deux fonctions qui sont elles mêmes composées de deux fonctions dérivables. On trouve :
est dérivable, comme combinaison linéaire de deux fonctions qui sont elles mêmes composées de deux fonctions dérivables. On trouve :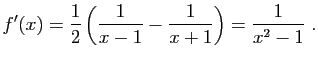 Pour
Pour dans
dans ![$ ]-\infty,-1[$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img480.gif) ou
ou ![$ ]1,+\infty[ $](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img481.gif) ,
, 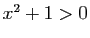 , donc
, donc 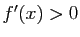 , donc
, donc  est strictement croissante sur ces intervalles. Pour
est strictement croissante sur ces intervalles. Pour  dans
dans ![$ ]-1,1[ $](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img442.gif) ,
, 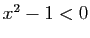 , donc
, donc 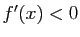 , donc
, donc  est strictement décroissante sur
est strictement décroissante sur ![$ ]-1,1[ $](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img442.gif) .
. - On trouve :
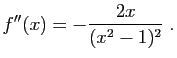 La dérivée seconde de
La dérivée seconde de est positive pour
est positive pour 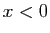 , négative pour
, négative pour 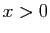 . Donc
. Donc  est convexe sur
est convexe sur ![$ ]-\infty,-1[$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img480.gif) et sur
et sur ![$ ]-1,0] $](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img482.gif) , concave sur
, concave sur 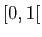 et sur
et sur ![$ ]1,+\infty[ $](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img481.gif) .
. - Démontration par récurrence. La formule est vraie pour
 :
: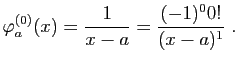 Supposons-la vraie pour
Supposons-la vraie pour . Alors :
. Alors :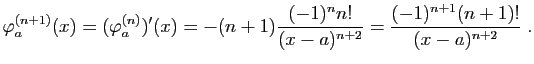 La formule est vraie pour
La formule est vraie pour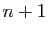 , elle est donc vraie pour tout
, elle est donc vraie pour tout  .
. - Pour
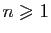 , la dérivée
, la dérivée  -ième de
-ième de  est la dérivée
est la dérivée 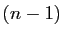 -ième de
-ième de 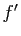 . Or :
. Or :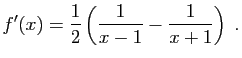 Par linéarité, on en déduit :
Par linéarité, on en déduit :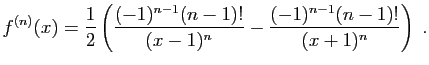
- On obtient :
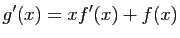 et
et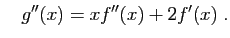 En utilisant les expressions des questions 1 et 2 :
En utilisant les expressions des questions 1 et 2 :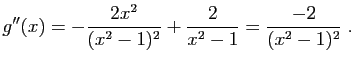 La dérivée seconde de
La dérivée seconde de est négative en tout point où elle est définie, donc
est négative en tout point où elle est définie, donc  est concave sur tout intervalle inclus dans
est concave sur tout intervalle inclus dans  .
. - La fonction
 est croissante sur
est croissante sur ![$ ]-\infty,-1[$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img480.gif) . Or la limite de
. Or la limite de  en
en  est nulle. Donc
est nulle. Donc  est positive sur
est positive sur ![$ ]-\infty,-1[ $](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img550.gif) . La fonction
. La fonction  est décroissante sur
est décroissante sur ![$ ]-1,0[$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img551.gif) . Or
. Or 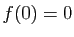 . Donc
. Donc  est positive sur
est positive sur ![$ ]-1,1[ $](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img442.gif) . Donc
. Donc 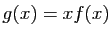 est négative pour tout
est négative pour tout  négatif.On montre de la même façon que
négatif.On montre de la même façon que est négative sur
est négative sur 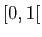 et sur
et sur ![$ ]1,+\infty[ $](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img481.gif) (ou bien en remarquant que pour tout
(ou bien en remarquant que pour tout 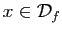 ,
, 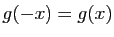 ). Donc :
). Donc :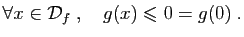 Donc
Donc admet bien un maximum global en 0. On constate que :
admet bien un maximum global en 0. On constate que :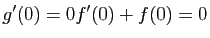 et
et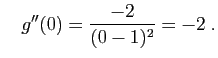 (Ceci entraîne que 0 est un maximum local, mais ne permet pas d'affirmer que c'est un maximum global).
(Ceci entraîne que 0 est un maximum local, mais ne permet pas d'affirmer que c'est un maximum global). - En utilisant la formule de Leibniz :
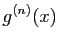
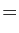
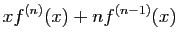
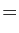
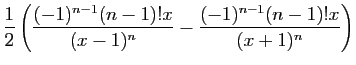
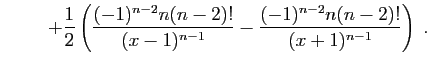
Exercice 3 :
- Par hypothèse, il existe
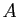 tel que pour tout
tel que pour tout 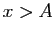 ,
, 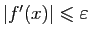 . Par le théorème des accroissements finis, pour tout
. Par le théorème des accroissements finis, pour tout 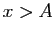 , il existe
, il existe ![$ c\in ]A,x[$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img563.gif) tel que :
tel que :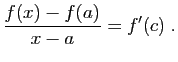 Puisque
Puisque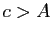 , on a bien :
, on a bien :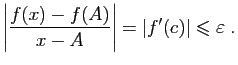
- Soit
 . Fixons
. Fixons  tel que pour tout
tel que pour tout  ,
,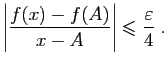 Pour
Pour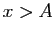 , écrivons :
, écrivons :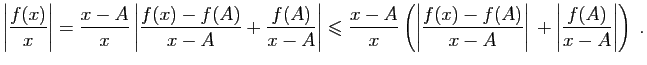 Or :
Or :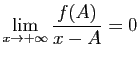 et
et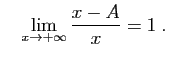 Il existe
Il existe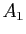 tel que pour tout
tel que pour tout 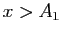 :
: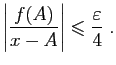 D'autre part, il existe
D'autre part, il existe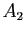 tel que pour tout
tel que pour tout 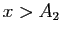 :
: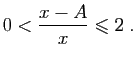 Pour tout
Pour tout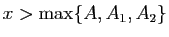 , on a donc :
, on a donc :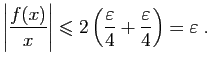 D'où le résultat.
D'où le résultat. - Soit
 la fonction qui à
la fonction qui à  associe
associe 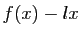 : elle est dérivable sur
: elle est dérivable sur ![$ ]0,+\infty[$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img357.gif) et
et 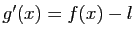 . Donc
. Donc 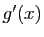 tend vers 0 quand
tend vers 0 quand  tend vers
tend vers 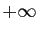 . D'après la question précédente, on a :
. D'après la question précédente, on a :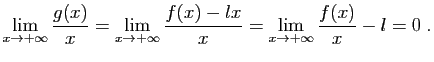 Donc :
Donc :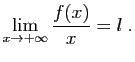
Newton et Leibniz
Les problèmes de quadrature (intégration) et de tangente (dérivation) ont passionné de nombreux mathématiciens depuis Archimède. Les premiers à avoir compris le rapport entre les deux sont Isaac Newton (1643-1727) et Gottfried Wilhem von Leibniz (1646-1716). Ils sont maintenant considérés comme co-inventeurs du calcul différentiel.Pourtant la controverse a longtemps fait rage, du vivant de Newton et Leibniz, et pendant encore de nombreuses années après leur mort. Les uns, à la suite de Newton lui-même, accusaient Leibniz de plagiat, car il aurait eu accès à des manuscrits non publiés de Newton. Les autres prouvaient sans conteste l'antériorité des publications de Leibniz et la supériorité de son système de notation. Il semble bien que Newton avait effectivement développé ses idées avant Leibniz, mais que, même si ce dernier a eu accès à des manuscrits de Newton, il a travaillé de façon indépendante. La controverse, qui paraît de nos jours plutôt futile, eut pour conséquence de couper pendant longtemps les mathématiciens anglais du reste de l'Europe : ce n'est qu'au début du XIXe siècle que les notations de Leibniz furent acceptées en Angleterre. Voici comment, dans Philosophiae Naturalis Principia Mathematica (1687), Newton exprime sa vision des dérivées.Les rapports ultimes dans lesquels les quantités disparaissent ne sont pas réellement des rapports de quantités ultimes, mais les limites vers lesquelles les rapports de quantités, décroissant sans limite, s'approchent toujours, et vers lesquelles ils peuvent s'approcher aussi près qu'on veut.La vision de Newton est très proche de notre définition moderne de la dérivée comme limite d'un taux d'accroissement. C'est d'autant plus remarquable que la notion de limite ne sera définie rigoureusement, que presque deux siècles après les premières découvertes de Newton. L'intuition de Newton est puissante, mais lui-même sent bien qu'il n'a pas défini ses quantités infinitésimales de manière suffisamment rigoureuse. D'ailleurs elles resteront longtemps pour beaucoup un «fantôme de quantités disparues». Peut-être est-ce une des raisons pour lesquelles Newton, dont les premiers travaux sur le sujet datent de 1664, n'achèvera son ouvrage «la méthode des fluxions et des suites infinies» qu'en 1671, et ne le publiera pas de son vivant... contrairement à Leibniz. Par un clin d' il de l'histoire, les noms de Newton et Leibniz sont restés attachés à deux formules extrêmement proches.
il de l'histoire, les noms de Newton et Leibniz sont restés attachés à deux formules extrêmement proches.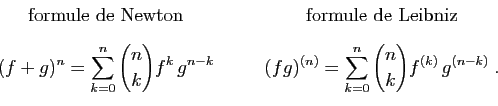
Le calcul différentiel indien
Le verset 12 des «Harmonies Célestes»1, écrit en 499 par Aryabhata est une collection de 24 nombres :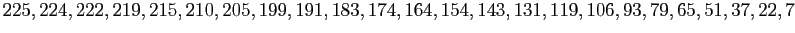 Il faut comprendre ces nombres comme les différences successives entre les demi-cordes des angles obtenus en divisant en 24 parties égales un quart de cercle de rayon 3428 (la somme des 24 valeurs). En clair : les 24 sommes cumulées, divisées par 3428 sont des valeurs approchées de
Il faut comprendre ces nombres comme les différences successives entre les demi-cordes des angles obtenus en divisant en 24 parties égales un quart de cercle de rayon 3428 (la somme des 24 valeurs). En clair : les 24 sommes cumulées, divisées par 3428 sont des valeurs approchées de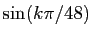 , pour
, pour 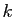 allant de 1 à 24. Faites le calcul : la différence maximale en valeur absolue entre les valeurs d'Aryabhata et les valeurs exactes est de
allant de 1 à 24. Faites le calcul : la différence maximale en valeur absolue entre les valeurs d'Aryabhata et les valeurs exactes est de 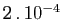 : pas si mal pour quelqu'un qui ne travaillait qu'avec des entiers ! Un peu plus loin, Aryabhata montre qu'il avait finement observé la décroissance de ses tables de différences : «Les différences sont diminuées des quotients successifs des sinus par le premier sinus». En clair, si
: pas si mal pour quelqu'un qui ne travaillait qu'avec des entiers ! Un peu plus loin, Aryabhata montre qu'il avait finement observé la décroissance de ses tables de différences : «Les différences sont diminuées des quotients successifs des sinus par le premier sinus». En clair, si 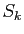 désigne la
désigne la 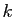 -ième valeur cumulée :
-ième valeur cumulée :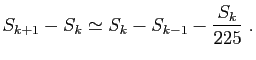 Ramené aux différences de sinus successifs, Aryabhata n'est pas loin d'exprimer un double taux d'accroissement :
Ramené aux différences de sinus successifs, Aryabhata n'est pas loin d'exprimer un double taux d'accroissement :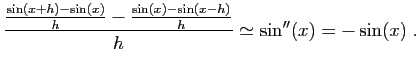 Mais parler de dérivée seconde au temps d'Aryabhata serait anachronique, d'autant plus que sa règle ne s'appliquait qu'aux multiples de
Mais parler de dérivée seconde au temps d'Aryabhata serait anachronique, d'autant plus que sa règle ne s'appliquait qu'aux multiples de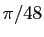 . Le premier astronome indien à formuler une règle de calcul approchée générale pour de petites différences de sinus est Manjula (932) :
. Le premier astronome indien à formuler une règle de calcul approchée générale pour de petites différences de sinus est Manjula (932) :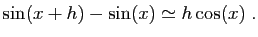 Cette règle empirique sera reprise par Aryabhata II (950) et Bhaskara II (1150). Ce dernier donne une justification géométrique de la formule, et est parfaitement conscient qu'elle est d'autant meilleure que
Cette règle empirique sera reprise par Aryabhata II (950) et Bhaskara II (1150). Ce dernier donne une justification géométrique de la formule, et est parfaitement conscient qu'elle est d'autant meilleure que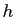 est petit : il parle à cette occasion d'«immesurablement petit». Il exprime même les notions de «différence instantanée de sinus» et «mouvement instantané». Cela suffit-il pour en faire l'inventeur des dérivées ? Peut-être pas car il ne dit jamais explicitement que le cosinus est la dérivée du sinus. Pourtant il est conscient du fait que quand une fonction atteint son maximum, sa «différence instantanée» s'annule. Il observe aussi que quand une planète est à son apogée ou à son périgée, la différence entre sa position observée et sa position prédite pour un mouvement uniforme s'annule et il en déduit qu'en un certain point intermédiaire l'incrément de cette quantité doit aussi s'annuler : c'est le théorème de Rolle !Du XIVe au XVIe siècle, à la suite de Madhava (1340-1425) une importante école d'astronomie fleurit dans l'état du Kérala, au Sud de l'Inde. Fidèles à la tradition de leurs ancêtres, ces astronomes développent encore le calcul différentiel. Ainsi le théorème des valeurs intermédiaires sera énoncé explicitement au XVe siècle par Parameshvara (1370-1460) dans «Lilavati Bhasya» qui est un commentaire du Lilavati de Bhaskara. Certains ont accusé Newton et Leibniz d'avoir, deux siècles plus tard, pillé les résultats des mathématiciens du Kérala. C'est oublier un peu vite que, malgré des algorithmes d'approximations impressionnants, ceux-ci n'ont jamais défini les notions de dérivée et d'intégrale, ni surtout établi leur réciprocité. Il n'existe aucune preuve que les résultats de l'école du Kérala aient été connus en dehors de l'Inde avant le XIXe siècle. Mais peut-être serez-vous tentés de répondre à la question « qui de Newton ou Leibniz a inventé le calcul infinitésimal ?» par : ni l'un ni l'autre !
est petit : il parle à cette occasion d'«immesurablement petit». Il exprime même les notions de «différence instantanée de sinus» et «mouvement instantané». Cela suffit-il pour en faire l'inventeur des dérivées ? Peut-être pas car il ne dit jamais explicitement que le cosinus est la dérivée du sinus. Pourtant il est conscient du fait que quand une fonction atteint son maximum, sa «différence instantanée» s'annule. Il observe aussi que quand une planète est à son apogée ou à son périgée, la différence entre sa position observée et sa position prédite pour un mouvement uniforme s'annule et il en déduit qu'en un certain point intermédiaire l'incrément de cette quantité doit aussi s'annuler : c'est le théorème de Rolle !Du XIVe au XVIe siècle, à la suite de Madhava (1340-1425) une importante école d'astronomie fleurit dans l'état du Kérala, au Sud de l'Inde. Fidèles à la tradition de leurs ancêtres, ces astronomes développent encore le calcul différentiel. Ainsi le théorème des valeurs intermédiaires sera énoncé explicitement au XVe siècle par Parameshvara (1370-1460) dans «Lilavati Bhasya» qui est un commentaire du Lilavati de Bhaskara. Certains ont accusé Newton et Leibniz d'avoir, deux siècles plus tard, pillé les résultats des mathématiciens du Kérala. C'est oublier un peu vite que, malgré des algorithmes d'approximations impressionnants, ceux-ci n'ont jamais défini les notions de dérivée et d'intégrale, ni surtout établi leur réciprocité. Il n'existe aucune preuve que les résultats de l'école du Kérala aient été connus en dehors de l'Inde avant le XIXe siècle. Mais peut-être serez-vous tentés de répondre à la question « qui de Newton ou Leibniz a inventé le calcul infinitésimal ?» par : ni l'un ni l'autre !Le dernier disciple de Galilée
Pour Vincenzio Viviani2, tout commence en 1639. Galilée, alors âgé de 75 ans et devenu aveugle, cherche quelqu'un pour l'aider dans ses travaux. À 17 ans, Viviani, issu d'une famille aisée de la noblesse florentine, se signale par son talent précoce pour les mathématiques. Galilée apprécie la tournure d'esprit et le goût pour les études du jeune homme, et en fait son pensionnaire à Arcetri, sur les collines de Florence. Jusqu'à la mort de Galilée trois ans plus tard, Viviani sera le lecteur et le secrétaire du grand homme. Galilée en vint à considérer Viviani comme un fils, et Viviani conçut pour celui qui l'avait ainsi adopté un attachement profond, qu'il manifesta pendant les 60 ans qu'il devait lui survivre, et même au-delà. Après la condamnation de Galilée par l'Inquisition, et l'interdiction faite de l'enterrer en terre consacrée, il faudra longtemps avant que ses restes puissent reposer dans le caveau familial de l'église Santa Croce à Florence. Ce ne fut fait qu'en 1737, 34 ans après la mort de Viviani qui avait laissé par testament des intructions précises pour l'édification du tombeau de Galilée, auprès duquel ses propres restes furent placés.Les trois ans passés auprès du vieux sage marquèrent définitivement Viviani, qui devint lui-même un savant reconnu, membre de plusieurs académies européennes, dont l'Académie des Sciences de Paris, où Fontenelle prononça son éloge.
Partout il se nomme le dernier disciple de Galilée [...] ; jamais il ne met son nom à un ouvrage sans l'accompagner de cette qualité ; jamais il ne manque une occasion de parler de Galilée et quelquefois même, ce qui fait encore mieux l'éloge de son c
Quant à l'homme, voici le portrait plutôt flatteur d'un contemporain. ur, il en parle sans beaucoup de nécessité ; jamais il ne nomme le nom de Galilée sans lui rendre un hommage ; et l'on sent bien que ce n'est point pour s'associer en quelque sorte au mérite de ce grand homme et en faire rejaillir une partie sur lui ; le style de la tendresse est bien aisé à reconnaître d'avec celui de la vanité.
ur, il en parle sans beaucoup de nécessité ; jamais il ne nomme le nom de Galilée sans lui rendre un hommage ; et l'on sent bien que ce n'est point pour s'associer en quelque sorte au mérite de ce grand homme et en faire rejaillir une partie sur lui ; le style de la tendresse est bien aisé à reconnaître d'avec celui de la vanité.
de m
Élève d'un des savants les plus novateurs de son époque, Viviani se signale pourtant par sa fidélité à la géométrie des classiques grecs3. Il s'était fait connaître pour avoir reconstitué un texte d'Appolonius, que l'on croyait perdu, mais qui fut retrouvé dans une traduction arabe avant que Viviani ait terminé son travail de divination. La proximité entre la traduction de l'original et la reconstitution de Viviani, établit la réputation de ce dernier. Grand connaisseur de Pappus, il sait que l'on trouve dans ses travaux la description d'une courbe, tracée sur une sphère, qui délimite sur cette sphère une surface quarrable, c'est-à-dire dont on peut donner l'aire exacte. Cette courbe est l'intersection avec la sphère d'un cylindre dont le diamètre est égal au rayon de la sphère, et dont une directrice passe par le centre de la sphère (figure 7). urs honnêtes et pures ; de manières exquises ; d'aspect agréable ; avec toujours un air de gaieté sur le visage ; modéré dans ses paroles, très apprécié dans sa conversation. Il était plutôt grand de taille, avait la peau claire et les cheveux bruns ; ses yeux d'un léger bleu turquoise étaient toujours vifs et brillants.
urs honnêtes et pures ; de manières exquises ; d'aspect agréable ; avec toujours un air de gaieté sur le visage ; modéré dans ses paroles, très apprécié dans sa conversation. Il était plutôt grand de taille, avait la peau claire et les cheveux bruns ; ses yeux d'un léger bleu turquoise étaient toujours vifs et brillants.
Figure 7: La fenêtre de Viviani 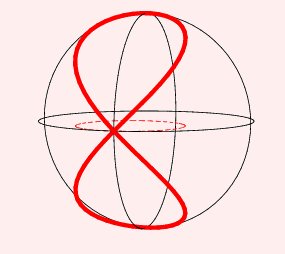 En 1692, connaissant la solution, il pose le problème comme un défi lancé aux tenants de la nouvelle pratique analytique, Leibniz en tête, qui prétendent que le tout nouveau calcul infinitésimal peut résoudre des problèmes sur lesquels la géométrie des Grecs échoue. L'année précédente, les frères Bernoulli et Leibniz avaient corrigé une erreur de Galilée sur la chaînette, ce qui a sans doute contribué à indisposer Viviani.ENIGME GEOMETRIQUE DE LA MERVEILLEUSE CONSTRUCTION DE LA VOUTE HEMISPHERIQUE QUARRABLEle 4 avril 1692, dont on espère la résolution par les arts secrets des fameux Analystes de l'âge présent, puisque l'homme versé seulement dans les travaux de la pure Géométrie est incapable, semble-t-il, d'accéder à de tels mystères.proposée par D. PIO LISCI PUSILLO, géomètre
En 1692, connaissant la solution, il pose le problème comme un défi lancé aux tenants de la nouvelle pratique analytique, Leibniz en tête, qui prétendent que le tout nouveau calcul infinitésimal peut résoudre des problèmes sur lesquels la géométrie des Grecs échoue. L'année précédente, les frères Bernoulli et Leibniz avaient corrigé une erreur de Galilée sur la chaînette, ce qui a sans doute contribué à indisposer Viviani.ENIGME GEOMETRIQUE DE LA MERVEILLEUSE CONSTRUCTION DE LA VOUTE HEMISPHERIQUE QUARRABLEle 4 avril 1692, dont on espère la résolution par les arts secrets des fameux Analystes de l'âge présent, puisque l'homme versé seulement dans les travaux de la pure Géométrie est incapable, semble-t-il, d'accéder à de tels mystères.proposée par D. PIO LISCI PUSILLO, géomètreParmi les vénérables monuments de la savante Grèce antique, se dresse encore, destiné à durer éternellement, un Temple très auguste à plan circulaire, dédié à la FECONDE GEOMETRIE, qui est recouvert d'une coupole parfaitement hémisphérique à l'intérieur ; mais dans cette coupole, quatre fenêtres d'aires égales (disposées autour et sur la base de l'hémisphère même) sont construites de telle configuration, de telle grandeur, avec une telle industrie et une telle intelligence que, celles-ci ôtées, la surface courbe restant de la coupole, ornée d'un travail précieux, peut être quarrée géométriquement.
On demande simplement quelle est cette partie quarrable de la surface hémisphérique tendue comme une voile marine gonflée, par quelle méthode ou par quel art fut-elle obtenue par l'Architecte Géomètre, et à quelle surface plane enfin elle est égale.
La résolution du présent problème (qui permet la contruction aussi bien que la quadrature de cette admirable voûte) a été offerte à son Altesse SérénissimeFERDINAND, Prince de Toscane, amateur et patron généreux des sciences et des arts nobles, par l'auteur même de l'énigme. Celui-ci du même coup ne doute point que le problème ne doive être trouvé aussitôt par chacun des illustres Analystes qui existent aujourd'hui dans le monde des lettres, en partageant en carrés appropriés cette remarquable voûte quarrable découpée sur l'hémisphère, et il attend impatiemment que, les subtiles recherches des mêmes et leurs multiples travaux se ramenant au même et unique [lieu] géométrique, alors ceux qui osent témérairement lancer des injures à la Géométrie apprennent à se taire, ou plutôt s'écrient à haute voix :
Ô unique Science des vérités accessibles, que l'Esprit divin a répandu dans l'esprit humain, afin que celle-ci méprisant les choses inaccessibles, changeantes et trompeuses, vise seulement les choses éternelles, qui sont toujours et pour tous semblables, et n'ait jamais pour son étude d'objet plus innocent.
Le nom d'emprunt sous lequel Viviani pose l'énigme est un anagramme de Postremo Galilaei Discipulo (le dernier disciple de Galilée). Il ne cache pas son ironie à l'égard des « illustres Analystes qui existent aujourd'hui». Mais ces derniers sont prompts à relever le défi, qui tombe à pic comme banc d'essai pour le calcul infinitésimal. Leibniz le résoud dit-il le jour même où il en prend connaissance, Jean Bernoulli publie 5 solutions différentes, Roberval dit avoir déjà rencontré la courbe, Huygens, le Marquis de l'Hôpital, Wallis et Gregory fournissent aussi des réponses. Voici un extrait de celle de Leibniz, qui profite de son triomphe pour faire un brin de propagande visionnaire.
Hippocrate de Chio a effectué la quadrature de sa lunule, déjà connue d'Aristote ; mais elle est plane et n'a de courbe que son périmètre. Les lunules sphériques (qu'on peut aussi appeler « voiles»), ne peuvent être projetées qu'à la perpendiculaire, et elles sont pourtant maintenant converties en figures rectilignes. Et la recherche d'Hippocrate n'était pas difficile ; la nôtre est beaucoup plus compliquée, surtout pour qui ignore les méthodes que nous utilisons.
[...] Pour nous le sujet nous a si bien réussi qu'à partir d'une surface sphérique donnée, nous pouvons en détacher des arches d'une grandeur donnée (en-dessous pourtant d'une certaine grandeur), ce qui est résoudre le problème posé d'une infinité de manières.
[...] Je souhaite - et ce souhait si d'autres y travaillent n'est pas irréalisable - voir la Géométrie réduite à l'Analyse absolue (si nous visons au plus haut) de sorte que le genre humain, délivré de cette difficulté, puisse appliquer désormais, pour son plus grand plaisir et son plus grand profit, son étude à la nature même et aux éléments concrets et puisse ainsi y reconnaître l'Étude Divine.
Si l'esprit humain, armé de la véritable méthode, se tourne sérieusement de ce côté, je ne doute point qu'il produira un jour de grandes merveilles pour vaincre les maladies, pour accroître les commodités de l'existence, pour connaître les miracles que Dieu fait dans la nature.
Les «fameux Analystes de l'âge présent», vainqueurs par KO, eurent la magnanimité de baptiser l'objet de l'énigme «fenêtre de Viviani». Elle s'ouvrait sur un avenir radieux : le Siècle des Lumières qui allait commencer serait bien en mathématiques celui des victoires du calcul différentiel.Règle de l'Hôpital et Théorème de Rolle
L'histoire est injuste. Nous vous avons proposé comme exercice facile d'application des définitions, la «Règle de l'Hôpital» : la limite du rapport de deux accroissements de fonctions en un point est le rapport des dérivées des fonctions en ce point ; et au cas où vous poseriez la question, non, il n'est vraiment pas utile de retenir ce résultat par c ur. En revanche, nous avons lourdement insisté sur l'importance du Théorème de Rolle, qui au fond n'est ni plus difficile ni moins intuitif : si une fonction part d'une valeur pour retourner à cette même valeur, sa dérivée doit s'annuler dans l'intervalle. En 1691, Guillaume François Antoine de L'Hôpital, marquis de Sainte-Mesme, comte d'Entremont, seigneur d'Oucques, La Chaise, Le Bréau et autres lieux (1661-1704), avait invité chez lui Jean Bernoulli, pour apprendre de celui-ci la nouvelle théorie de Leibniz. L'ayant bien assimilée, il s'en était fait l'ardent propagandiste, publiant en 1696 son «Analyse des infiniment petits, pour l'intelligence des lignes courbes». Cet ouvrage fit beaucoup pour la diffusion de la théorie en France, même si celle-ci n'alla pas sans heurts 4. Voici le début lyrique de la préface de l'«Analyse des Infiniment Petits».
ur. En revanche, nous avons lourdement insisté sur l'importance du Théorème de Rolle, qui au fond n'est ni plus difficile ni moins intuitif : si une fonction part d'une valeur pour retourner à cette même valeur, sa dérivée doit s'annuler dans l'intervalle. En 1691, Guillaume François Antoine de L'Hôpital, marquis de Sainte-Mesme, comte d'Entremont, seigneur d'Oucques, La Chaise, Le Bréau et autres lieux (1661-1704), avait invité chez lui Jean Bernoulli, pour apprendre de celui-ci la nouvelle théorie de Leibniz. L'ayant bien assimilée, il s'en était fait l'ardent propagandiste, publiant en 1696 son «Analyse des infiniment petits, pour l'intelligence des lignes courbes». Cet ouvrage fit beaucoup pour la diffusion de la théorie en France, même si celle-ci n'alla pas sans heurts 4. Voici le début lyrique de la préface de l'«Analyse des Infiniment Petits».
L'ANALYSE qu'on explique dans cet ouvrage, suppose la commune ; mais elle en est fort différente. L'Analyse ordinaire ne traite que des grandeurs finies : celle-ci pénètre jusque dans l'infini même. Elle compare les différences infiniment petites des grandeurs finies ; elle découvre les rapports de ces différences : et par là elle fait connaître ceux des grandeurs finies, qui comparées avec ces infiniment petits sont comme autant d'infinis. On peut même dire que cette Analyse s'étend au-delà de l'infini : car elle ne se borne pas aux différences infiniment petites ; mais elle découvre les rapports des différences de ces différences, ceux encore des différences troisièmes, quatrièmes, et ainsi de suite, sans trouver jamais de terme qui la puisse arrêter. De sorte qu'elle n'embrasse pas seulement l'infini ; mais l'infini de l'infini, ou une infinité d'infinis.
Rassurez-vous : beaucoup de lecteurs de l'époque ont ressenti le même vertige que vous devant une telle envolée. Cette nouvelle analyse supposée s'étendre «au-delà de l'infini», sans que l'on ait donné de sens rigoureux à son objet de base, les « différences infiniment petites», ressemblait fort à un château dans les nuages, et beaucoup doutaient en conséquence que l'on puisse en tirer autre chose que du vent. En 1701, Michel Rolle (1652-1719) lit à l'Académie Royale des Sciences un mémoire intitulé «Du nouveau système de l'infini». Dès les premières lignes, le ton est donné.
On avait toujours regardé la Géométrie comme une Science exacte, et même comme la source de l'exactitude qui est répandue dans toutes les autres parties des Mathématiques. On ne voyait parmi ses principes que de véritables axiomes : tous les théorèmes et tous les problèmes qu'on y proposait étaient ou solidement démontrés, ou capables d'une solide démonstration ; et s'il s'y glissait quelques propositions ou fausses ou peu certaines, aussitôt on les bannissait de cette science.
Mais il semble que ce caractère d'exactitude ne règne plus dans la Géométrie depuis que l'on y a mêlé le nouveau système des infiniment petits. Pour moi, je ne vois pas qu'il ait rien produit pour la vérité, et il me paraît qu'il couvre souvent l'erreur.
Voici comment Fontenelle, bien des années plus tard, rapporte la controverse dans son éloge de Rolle.
En ce temps-là, le livre de M. le Marquis de l'Hôpital avait paru, et presque tous les mathématiciens commençaient à se tourner du côté de la nouvelle géométrie de l'infini, jusque-là peu connue. L'universalité surprenante des démontrations, la finesse et la promptitude des solutions les plus difficiles, une nouveauté singulière et imprévue, tout attirait les esprits, et il se faisait dans le monde géomètre une révolution bien marquée. Elle n'était pourtant pas absolument générale ; dans le pays même des démonstrations on trouve encore le moyen de se diviser. Feu M. L'Abbé Galois, comme nous l'avons dit même dans son éloge, ne goûtait point la nouvelle Géométrie, mais il était bien aise de ne la combattre qu'avec le secours ou à l'abri d'un géomètre de nom, et heureusement il trouva dans M. Rolle les dispositions nécessaires pour s'unir à lui. Il mit dans la société le courage d'entreprendre la guerre, et l'art de la conduire, qui tous deux auraient peut-être manqué à M. Rolle, et celui-ci ne fut obligé que de fournir les raisonnements.
[...]
Quand la paix des Infiniment-petits fut faite, ou le silence ordonné, M. Rolle donna son application à d'autres sujets de Géométrie, où l'algèbre dominait toujours ; il ne laissait pas d'y glisser encore adroitement des accusations d'insuffisance ou même de fausseté contre le nouveau calcul, avec lequel il ne s'est jamais bien réconcilié, et les Infinitaires étaient au guet pour ne lui rien passer qui les intéressât trop.
Avant de combattre les «Infinitaires», M. Rolle avait quand même bien produit des mathématiques. Dans un ouvrage de 1691 «Démonstration d'une méthode pour résoudre les égalités de tous degrés», il avait exposé une technique pour localiser les racines d'un polynôme, la «méthode des cascades». Ce n'est que bien plus tard que l'on s'est rendu compte que la « cascade» d'un polynôme n'était autre que sa dérivée, et que l'observation qu'entre deux racines d'un polynôme on trouvait toujours une racine de sa dérivée, avait une portée beaucoup plus générale.Non, le Théorème de Rolle n'est pas vraiment dû à Michel Rolle ; mais que cela ne vous empêche pas de le retenir !Une construction de l'exponentielle et du logarithme
Le logarithme népérien vous a sans doute été présenté comme la primitive de la fonction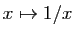 qui s'annule en
qui s'annule en 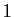 , et l'exponentielle comme sa fonction réciproque. On en déduit alors les propriétés de ces deux fonctions. Nous allons voir une autre définition.Le but de ce qui suit est de construire les fonctions exponentielle et logarithme, et d'en démontrer les principales propriétés, à partir de la propriété fondamentale de l'exponentielle, qui est de transformer les sommes en produit.
, et l'exponentielle comme sa fonction réciproque. On en déduit alors les propriétés de ces deux fonctions. Nous allons voir une autre définition.Le but de ce qui suit est de construire les fonctions exponentielle et logarithme, et d'en démontrer les principales propriétés, à partir de la propriété fondamentale de l'exponentielle, qui est de transformer les sommes en produit.
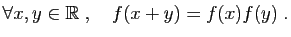
(3)
Cette construction illustrera l'utilisation des outils de base de l'analyse : limites, continuité, dérivabilité, convexité. Dans un premier temps, nous raisonnerons par condition nécessaire, en supposant l'existence d'une fonction vérifiant (3), pour en déduire ses propriétés.
vérifiant (3), pour en déduire ses propriétés.
Proposition 10 Soit une fonction de
une fonction de  dans
dans  , vérifiant (3). Alors :
, vérifiant (3). Alors :
- Si
 s'annule en un point, alors
s'annule en un point, alors  est identiquement nulle sur
est identiquement nulle sur  .
. - Si
 ne s'annule pas, alors
ne s'annule pas, alors 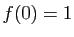 et pour tout
et pour tout 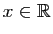 :
: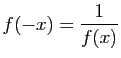
- Pour tout
 , pour tout
, pour tout  :
: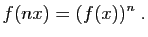
Démonstration : Si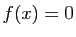 , alors pour tout
, alors pour tout  ,
,
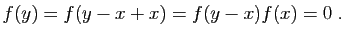
Donc, soit est identiquement nulle, soit elle ne s'annule jamais. Comme
est identiquement nulle, soit elle ne s'annule jamais. Comme 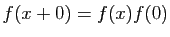 , si
, si 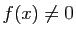 , alors
, alors 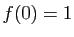 . Ensuite,
. Ensuite,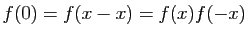 , d'où le point 2. Le point 3 se vérifie aussi facilement, par récurrence sur
, d'où le point 2. Le point 3 se vérifie aussi facilement, par récurrence sur  .
. 
Proposition 11 Soit une fonction de
une fonction de  dans
dans  , non nulle, continue en 0, et vérifiant (3). Alors
, non nulle, continue en 0, et vérifiant (3). Alors  est :
est :
- strictement positive,
- continue sur
 ,
, - convexe sur
 ,
, - dérivable sur
 et :
et :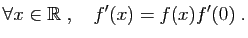
Démonstration : D'après la proposition 10, si est non nulle, alors
est non nulle, alors 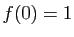 . Comme
. Comme  est continue en 0, il existe
est continue en 0, il existe  tel que pour tout
tel que pour tout ![$ x\in ]-\eta,\eta[ $](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img615.gif) ,
,  . Soit
. Soit 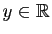 quelconque ; il existe
quelconque ; il existe 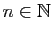 tel que
tel que ![$ y/n\in ]- \eta,\eta[ $](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img617.gif) . D'après le point 3 de la proposition 10,
. D'après le point 3 de la proposition 10, 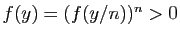 .Montrons maintenant la continuité en un point
.Montrons maintenant la continuité en un point  quelconque de
quelconque de  .
.
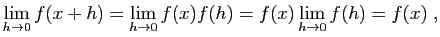
car est continue en 0 et
est continue en 0 et 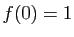 .La démonstration de la convexité est plus difficile. Nous souhaitons montrer que pour tout
.La démonstration de la convexité est plus difficile. Nous souhaitons montrer que pour tout 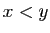 , et pour tout
, et pour tout ![$ \lambda\in[0,1]$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img239.gif) ,
,
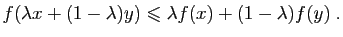
(4)
Nous allons d'abord montrer que pour tout ,
,

(5)
D'après (3) et le point 3 de la proposition 10,
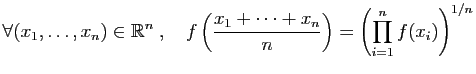
On pourrait en déduire (5), en utilisant... la concavité du logarithme, que nous sommes précisément en train de construire. Ce ne serait pas de jeu !Nous allons démontrer (5) par récurrence sur . Observons d'abord que (5) est trivialement vraie pour
. Observons d'abord que (5) est trivialement vraie pour  . Vérifions qu'elle est vraie pour
. Vérifions qu'elle est vraie pour  . D'après (3) et puisque
. D'après (3) et puisque  est strictement positive, on a :
est strictement positive, on a :
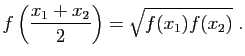
Il est facile de vérifier que si et
et 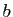 sont deux réels positifs, alors
sont deux réels positifs, alors 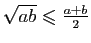 , d'où (5) pour
, d'où (5) pour  . Nous en déduisons ensuite que si (5) est vraie pour un entier
. Nous en déduisons ensuite que si (5) est vraie pour un entier  , alors elle est vraie pour
, alors elle est vraie pour  . En effet :
. En effet :
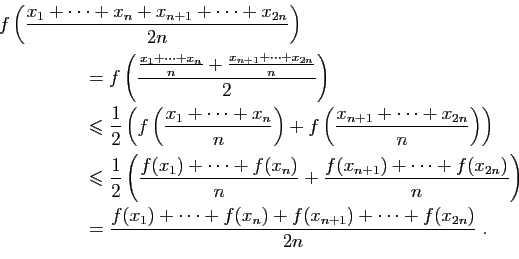
Montrons maintenant que si (5) est vraie pour un entier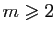 , alors elle est vraie pour
, alors elle est vraie pour 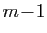 .
. 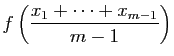
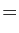
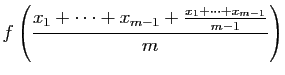
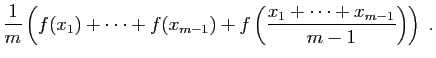
Soit en regroupant les termes :
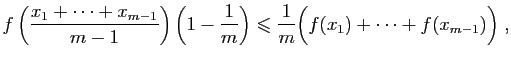
d'où le résultat pour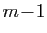 . Maintenant, si (5) est vraie pour un entier
. Maintenant, si (5) est vraie pour un entier  , elle est vraie pour
, elle est vraie pour 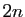 , et d'après ce qui précède, aussi pour
, et d'après ce qui précède, aussi pour 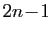 ,
, 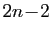 , ...,
, ..., 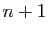 . Elle est donc vraie pour tout
. Elle est donc vraie pour tout  .Soient
.Soient  et
et  deux entiers positifs tels que
deux entiers positifs tels que 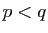 , et
, et  deux réels tels que
deux réels tels que 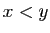 . Appliquons (5) pour
. Appliquons (5) pour 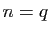 ,
, 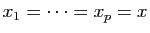 , et
, et 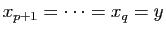 . On obtient :
. On obtient :
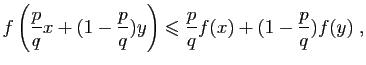
soit (4) pour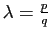 . Donc (4) est vraie pour tout
. Donc (4) est vraie pour tout 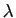 rationnel. Mais tout réel étant limite d'une suite de rationnels, et la fonction
rationnel. Mais tout réel étant limite d'une suite de rationnels, et la fonction  étant continue, (4) est aussi vraie pour tout
étant continue, (4) est aussi vraie pour tout 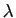 réel, donc
réel, donc  est convexe.La dérivabilité se déduit de la convexité, en utilisant la propriété (3). Commençons par montrer que
est convexe.La dérivabilité se déduit de la convexité, en utilisant la propriété (3). Commençons par montrer que  est dérivable en 0. Considérons la fonction
est dérivable en 0. Considérons la fonction 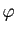 , qui à
, qui à 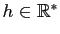 associe l'accroissement :
associe l'accroissement :
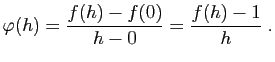
La fonction étant convexe, ses accroissements sont croissants, donc la fonction
étant convexe, ses accroissements sont croissants, donc la fonction  admet une limite à gauche et une limite à droite en 0. La fonction
admet une limite à gauche et une limite à droite en 0. La fonction  est donc dérivable à gauche et à droite en 0. Nous devons montrer que les deux dérivées sont égales. Pour cela, calculons
est donc dérivable à gauche et à droite en 0. Nous devons montrer que les deux dérivées sont égales. Pour cela, calculons  , en utilisant le point 2 de la proposition 10.
, en utilisant le point 2 de la proposition 10.
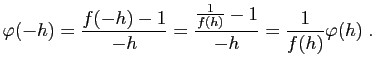
Or quand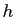 tend vers 0,
tend vers 0, 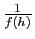 tend vers
tend vers  , par continuité de
, par continuité de  en 0. Donc la limite à gauche de
en 0. Donc la limite à gauche de 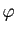 en 0 est égale à sa limite à droite, ce qui entraîne que
en 0 est égale à sa limite à droite, ce qui entraîne que  est dérivable en0. Pour en déduire la dérivabilité en un point
est dérivable en0. Pour en déduire la dérivabilité en un point  quelconque de
quelconque de  , il suffit d'appliquer une fois de plus la propriété (3) :
, il suffit d'appliquer une fois de plus la propriété (3) :
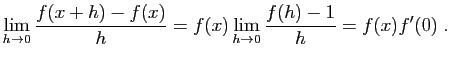
Puisque est strictement positive,
est strictement positive, 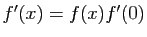 est de signe constant. La fonction
est de signe constant. La fonction  est :
est :- strictement croissante si
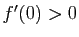 ,
, - constante (et égale à
 ) si
) si 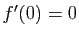 ,
, - strictement décroissante si
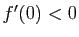 .
.
 Jusqu'ici nous n'avons raisonné que par condition nécessaire : rien ne prouve encore qu'il existe des fonctions
Jusqu'ici nous n'avons raisonné que par condition nécessaire : rien ne prouve encore qu'il existe des fonctions  vérifiant les hypothèses des deux propositions précédentes.
vérifiant les hypothèses des deux propositions précédentes.
Proposition 12 Pour tout , il existe une unique fonction
, il existe une unique fonction  , continue en 0, vérifiant (3), et telle que
, continue en 0, vérifiant (3), et telle que 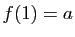 .
.
Démonstration : La fonction qui répond à la question est évidemment celle qui à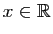 associe
associe 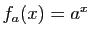 . Encore faut-il préciser sa définition, et montrer qu'elle est la seule.Si
. Encore faut-il préciser sa définition, et montrer qu'elle est la seule.Si  est un entier positif,
est un entier positif, 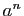 est le produit de
est le produit de  facteurs égaux à
facteurs égaux à  , et
, et 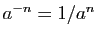 . La fonction qui à
. La fonction qui à  associe
associe 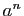 est strictement croissante et bijective de
est strictement croissante et bijective de  dans
dans . Donc sa réciproque est aussi strictement croissante et bijective de
. Donc sa réciproque est aussi strictement croissante et bijective de  dans
dans 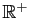 . Si
. Si  est un réel positif, le réel
est un réel positif, le réel 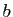 tel que
tel que 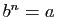 est donc défini de façon unique, et on convient de le noter
est donc défini de façon unique, et on convient de le noter 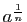 , de sorte que
, de sorte que 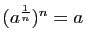 . Si
. Si 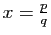 est un rationnel, nous savons donc définir
est un rationnel, nous savons donc définir 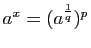 . Cette définition, et les propriétés des puissances entières, entraînent que la propriété (3) est vérifiée pour tout couple
. Cette définition, et les propriétés des puissances entières, entraînent que la propriété (3) est vérifiée pour tout couple  de rationnels :
de rationnels : 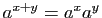 .
.
Nous souhaitons étendre la définition de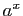 à tous les réels, par continuité. Observons d'abord que nous pouvons, sans perte de généralité, supposer que
à tous les réels, par continuité. Observons d'abord que nous pouvons, sans perte de généralité, supposer que 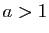 et
et 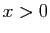 , grâce à la propriété
, grâce à la propriété 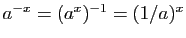 . Si
. Si  et
et 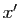 sont deux rationnels tels que
sont deux rationnels tels que 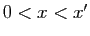 , alors
, alors 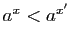 . Une des propriétés fondamentales de l'ensemble
. Une des propriétés fondamentales de l'ensemble  est que tout réel est la borne supérieure de l'ensemble des rationnels qui lui sont inférieurs. Si
est que tout réel est la borne supérieure de l'ensemble des rationnels qui lui sont inférieurs. Si  est un réel quelconque et
est un réel quelconque et 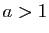 , nous pouvons donc définir
, nous pouvons donc définir 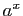 comme :
comme :
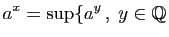 et
et 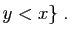
Il reste à vérifier que la fonction ainsi définie est bien continue, et qu'on a donc aussi :
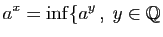 et
et 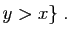
Pour cela, commençons par montrer que si est une suite de rationnels positifs, tendant vers 0, alors
est une suite de rationnels positifs, tendant vers 0, alors  converge vers
converge vers 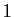 . Fixons
. Fixons 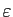 tel que
tel que 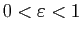 . Considérons les deux suites
. Considérons les deux suites 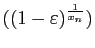 et
et 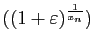 . Si la suite
. Si la suite 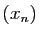 tend vers 0, la suite
tend vers 0, la suite 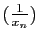 tend vers
tend vers 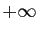 . Si
. Si 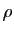 est un réel positif, alors quand
est un réel positif, alors quand 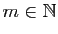 tend vers l'infini,
tend vers l'infini, 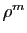 tend vers 0 si
tend vers 0 si 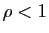 , vers
, vers 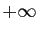 si
si  . On en déduit que
. On en déduit que 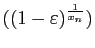 converge vers 0, alors que
converge vers 0, alors que 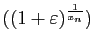 converge vers
converge vers 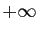 . Donc il existe
. Donc il existe 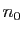 tel que pour tout
tel que pour tout 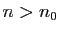 ,
,
![$\displaystyle a\in [(1-\varepsilon)^{\frac{1}{x_n}}) , (1+\varepsilon)^{\frac{1}{x_n}}],
$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img691.gif)
soit![$ a^{x_n}\in [1-\varepsilon,1+\varepsilon]$](http://ljk.imag.fr/membres/Bernard.Ycart/mel/dc/img692.gif) . Si les
. Si les 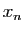 sont des rationnels négatifs, la conclusion est la même car
sont des rationnels négatifs, la conclusion est la même car 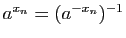 . Donc la conclusion reste vraie pour une suite de rationnels
. Donc la conclusion reste vraie pour une suite de rationnels 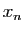 de signe quelconque. On en déduit donc que la fonction que nous avons définie est bien continue en 0.Pour
de signe quelconque. On en déduit donc que la fonction que nous avons définie est bien continue en 0.Pour 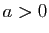 , la fonction qui à
, la fonction qui à  associe
associe 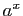 est donc continue en 0, elle est non nulle, et elle vérifie (3) pour tout
est donc continue en 0, elle est non nulle, et elle vérifie (3) pour tout 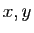 rationnels, donc pour tout
rationnels, donc pour tout 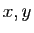 réels, en passant à la limite. D'après le point 2 de la proposition 11, elle est donc continue sur
réels, en passant à la limite. D'après le point 2 de la proposition 11, elle est donc continue sur  .
.
Pour l'unicité, il suffit d'observer que si une fonction vérifie (3) et est telle que
vérifie (3) et est telle que 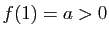 , alors par la proposition 10, elle est telle que
, alors par la proposition 10, elle est telle que 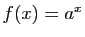 , pour tout
, pour tout  rationnel. Deux fonctions continues qui coïncident sur les rationnels, sont nécessairement égales (tout réel est limite d'une suite de rationnels). Donc
rationnel. Deux fonctions continues qui coïncident sur les rationnels, sont nécessairement égales (tout réel est limite d'une suite de rationnels). Donc 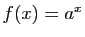 , pour tout
, pour tout  réel.
réel.  Pour
Pour  , notons
, notons  l'unique fonction continue en 0, vérifiant (3), et telle que
l'unique fonction continue en 0, vérifiant (3), et telle que 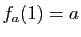 , à savoir la fonction qui à
, à savoir la fonction qui à 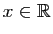 associe
associe 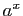 .
.
Puisque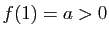 , la fonction
, la fonction  est non nulle et on peut lui appliquer la proposition 11 :
est non nulle et on peut lui appliquer la proposition 11 : 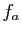 est dérivable sur
est dérivable sur  .
.
Définition 8 On appelle logarithme, et on note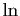 la fonction définie sur
la fonction définie sur  , qui à
, qui à 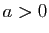 associe
associe 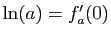 .
.
Proposition 13
- Pour tout
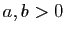 , on a :
, on a :
- Pour tout
 et
et 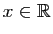 , on a :
, on a :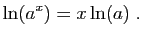
- La fonction
 est strictement croissante, et :
est strictement croissante, et :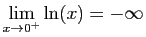 et
et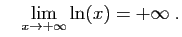
Démonstration : Pour le premier point, soient et
et 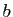 deux réels strictement positifs, et considérons la fonction
deux réels strictement positifs, et considérons la fonction 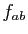 . On a :
. On a :
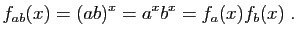
On calcule donc la dérivée de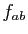 en 0, en dérivant le produit
en 0, en dérivant le produit 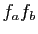 :
:
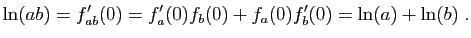
Pour le point 2, soit et
et 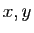 deux réels.
deux réels.
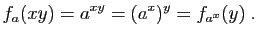
Fixons , dérivons par rapport à
, dérivons par rapport à  et prenons la dérivée en 0. On obtient :
et prenons la dérivée en 0. On obtient :
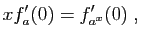
d'où le résultat.Passons au point 3. Fixons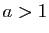 . La fonction
. La fonction 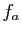 est alors strictement croissante, elle admet donc une limite en
est alors strictement croissante, elle admet donc une limite en 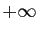 . Or la suite
. Or la suite 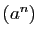 tend vers
tend vers 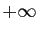 , donc la limite de
, donc la limite de 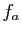 en
en 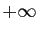 est
est 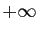 . La relation
. La relation 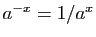 montre que la limite de
montre que la limite de  en
en  est 0. La fonction
est 0. La fonction  est donc bijective, de
est donc bijective, de  dans
dans 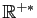 . La relation
. La relation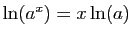 montre que la fonction réciproque de
montre que la fonction réciproque de 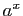 est la fonction qui à
est la fonction qui à 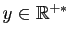 associe
associe 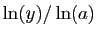 . Cette fonction est donc strictement croissante et bijective de
. Cette fonction est donc strictement croissante et bijective de  dans
dans  .
.  Il nous reste à définir la fonction exponentielle, qui est la réciproque du logarithme. D'après le point 3 de la proposition 13, il existe un réel unique, strictement positif, dont le logarithme vaut
Il nous reste à définir la fonction exponentielle, qui est la réciproque du logarithme. D'après le point 3 de la proposition 13, il existe un réel unique, strictement positif, dont le logarithme vaut  . On le note
. On le note  .
.
Définition 9 On appelle exponentielle, et on note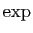 , la fonction qui à
, la fonction qui à 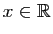 associe
associe 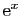 , où
, où 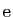 est l'unique réel tel que
est l'unique réel tel que 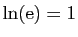 .
.
Proposition 14 L'exponentielle est la réciproque du logarithme. Les deux fonctions sont strictement croissantes et dérivables.
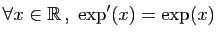 et
et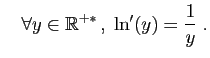
Puisque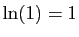 , on a
, on a 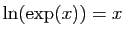 , par le point 2 de la proposition 13. La dérivée de l'exponentielle est donnée par le point 4 de la proposition 11. On dérive le logarithme comme une fonction réciproque :
, par le point 2 de la proposition 13. La dérivée de l'exponentielle est donnée par le point 4 de la proposition 11. On dérive le logarithme comme une fonction réciproque : - Si

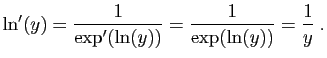
Aucun commentaire:
Enregistrer un commentaire